We shall merely provide a sketch of the argument. Let 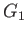 and
and 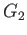 be two given groups.
A word is by definition a finite sequence
be two given groups.
A word is by definition a finite sequence
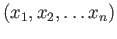 such that each
such that each 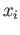 (
(
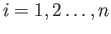 ) belongs to one of the groups,
no pair of adjacent terms of the sequence belong
to the same group and none of the
) belongs to one of the groups,
no pair of adjacent terms of the sequence belong
to the same group and none of the 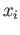 is the identity element of either of the groups.
We call the integer
is the identity element of either of the groups.
We call the integer  the length of the word and also include
the empty word of length zero. Denoting by
the length of the word and also include
the empty word of length zero. Denoting by 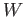 is the set of all words, the idea is to define a binary
operation of juxtaposition of words. The empty word would serve as the identity and the inverse of a word
is the set of all words, the idea is to define a binary
operation of juxtaposition of words. The empty word would serve as the identity and the inverse of a word
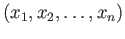 would be the word
would be the word
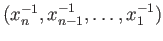 . One would hope that the operation of juxtaposition would make
. One would hope that the operation of juxtaposition would make 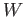 a group. This however would not quite
suffice. The juxtaposition of two words
a group. This however would not quite
suffice. The juxtaposition of two words
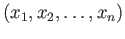 and
and
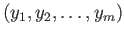 may result in a sequence that does not qualify to
be called a word for the simple reason that
may result in a sequence that does not qualify to
be called a word for the simple reason that 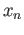 and
and 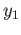 may belong to the same group.
When this happens we may try to replace the juxtaposed
string by the smaller string
may belong to the same group.
When this happens we may try to replace the juxtaposed
string by the smaller string
where
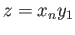 . If
. If 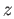 is not the unit element we do get a legitimate word but if
is not the unit element we do get a legitimate word but if 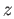 is the
unit element of one of the groups we must drop it altogether obtaining instead the still smaller string
is the
unit element of one of the groups we must drop it altogether obtaining instead the still smaller string
If 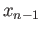 and
and 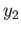 belong to the same group the above process must continue and thus in finitely many steps we obtain a legitimate word that
ought to be the product of the two given words. To check that we do get a group that qualifies as the coproduct of the given groups can be tedious.
The reader may consult [11], pp 72-73.
belong to the same group the above process must continue and thus in finitely many steps we obtain a legitimate word that
ought to be the product of the two given words. To check that we do get a group that qualifies as the coproduct of the given groups can be tedious.
The reader may consult [11], pp 72-73.
We now introduce the notion of a direct sum of abelian groups which will play a crucial role in the second
part of the
course.
nisha
2012-03-20