Suppose given a pair of morphisms
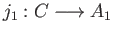 and
and
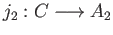 in a category
in a category
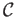 , represented as a diagram:
a push out is an object
, represented as a diagram:
a push out is an object 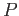 in
in 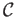 together with a pair of morphisms
together with a pair of morphisms
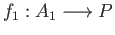 and
and
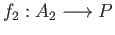 satisfying the following two conditions:
satisfying the following two conditions:
(i)
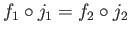
(ii) Universal property: Given any pair of morphisms
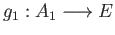 and
and
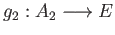 satisfying
satisfying
there exists a unique morphism
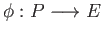 such that
such that
in
nisha
2012-03-20
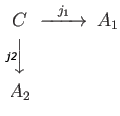
![]()
![]() and
and
![]() satisfying
satisfying