Next: Vector Spaces Up: Linear Algebra Previous: Miscellaneous Exercises Contents
Consider the problem of finding the set
of points of intersection of
the two planes
![]() and
and
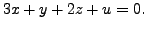
Let ![]() be the set of points of intersection of the
two planes. Then
be the set of points of intersection of the
two planes. Then ![]() has the
following properties:
has the
following properties:
Similarly, for an
![]() real matrix
real matrix ![]() consider
the set
consider
the set ![]() of solutions of the homogeneous linear system
of solutions of the homogeneous linear system
![]() This set satisfies the following properties:
This set satisfies the following properties:
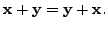
Thus we are lead to the following.