EXAMPLE 3.1.4
- The set
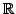 of real numbers, with the usual
addition and multiplication (i.e.,
of real numbers, with the usual
addition and multiplication (i.e.,
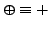 and
and
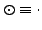 )
forms a vector space over
)
forms a vector space over
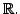
- Consider the set
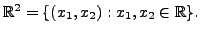 For
For
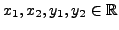 and
and
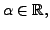 define,
define,
Then
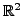 is a real vector space.
is a real vector space.
- Let
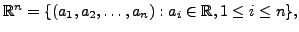 be the set of
be the set of 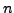 -tuples of real numbers. For
-tuples of real numbers. For
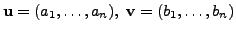 in
in  and
and
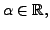 we define
we define
(called component wise or
coordinate wise operations).
Then  is a real vector
space with addition and scalar multiplication defined as above.
This vector space is denoted by
is a real vector
space with addition and scalar multiplication defined as above.
This vector space is denoted by
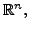 called the
real vector space of
called the
real vector space of 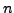 -tuples.
-tuples.
- Let
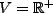 (the
set of positive real numbers). This is NOT A VECTOR SPACE
under usual operations of addition and scalar multiplication
(why?). We now define a new vector addition and scalar
multiplication as
(the
set of positive real numbers). This is NOT A VECTOR SPACE
under usual operations of addition and scalar multiplication
(why?). We now define a new vector addition and scalar
multiplication as
for all
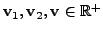 and
and
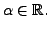 Then
Then
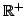 is a real vector space with
is a real vector space with 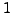 as
the additive identity.
as
the additive identity.
- Let
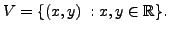 Define
Define
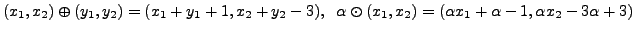 for
for
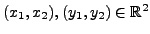 and
and
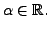 Then it can be easily verified that the vector
Then it can be easily verified that the vector 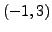 is the
additive identity and
is the
additive identity and  is indeed a real vector space.
is indeed a real vector space.
Recall 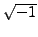 is denoted
is denoted 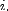
- Consider the set
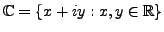 of
complex numbers.
of
complex numbers.
- For
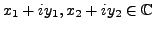 and
and
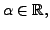 define,
define,
Then
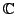 is a real vector space.
is a real vector space.
- For
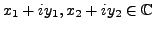 and
and
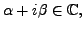 define,
define,
Then
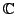 forms a complex vector space.
forms a complex vector space.
- Consider
the set
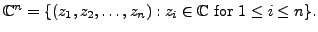 For
For
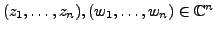 and
and
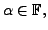 define,
define,
- If the set
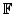 is the set
is the set
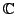 of complex numbers, then
of complex numbers, then
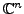 is
a complex vector space having
is
a complex vector space having 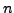 -tuple of complex numbers
as its vectors.
-tuple of complex numbers
as its vectors.
- If the set
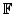 is the set
is the set
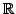 of real numbers, then
of real numbers, then
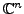 is
a real vector space having
is
a real vector space having 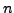 -tuple of complex numbers
as its vectors.
-tuple of complex numbers
as its vectors.
Remark 3.1.5
In Example 7a, the scalars are Complex
numbers and hence
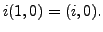 Whereas, in
Example 7b, the scalars are Real Numbers and
hence WE CANNOT WRITE
Whereas, in
Example 7b, the scalars are Real Numbers and
hence WE CANNOT WRITE
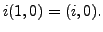
- Fix a positive integer
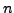 and let
and let
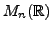 denote the set of all
denote the set of all
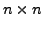 matrices with real entries.
Then
matrices with real entries.
Then
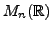 is a real vector space with vector addition and scalar multiplication defined by
is a real vector space with vector addition and scalar multiplication defined by
- Let
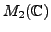 denote the set of all
denote the set of all
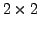 matrices with complex entries.
Then
matrices with complex entries.
Then
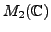 is a real vector space as well as a complex vector sapce
with vector addition and scalar multiplication defined by
is a real vector space as well as a complex vector sapce
with vector addition and scalar multiplication defined by
- Fix a positive integer
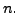 Consider the set,
Consider the set,
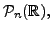 of all polynomials of degree
of all polynomials of degree 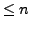 with coefficients from
with coefficients from
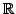 in the indeterminate
in the indeterminate 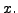 Algebraically,
Algebraically,
Let
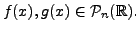 Then
Then
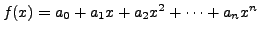 and
and
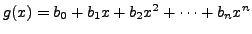 for some
for some
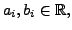
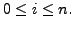 It can be verified that
It can be verified that
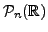 is a real
vector space with the addition and scalar multiplication defined
by:
is a real
vector space with the addition and scalar multiplication defined
by:
- Consider the set
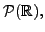 of all polynomials with
real coefficients. Let
of all polynomials with
real coefficients. Let
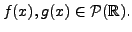 Observe that a
polynomial of the form
Observe that a
polynomial of the form
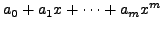 can be written as
can be written as
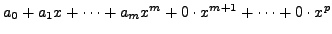 for any
for any 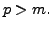 Hence, we can assume
Hence, we can assume
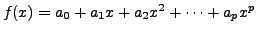 and
and
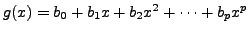 for some
for some
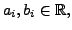
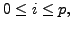 for some large positive integer
for some large positive integer 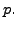 We
now define the vector addition and scalar multiplication as
We
now define the vector addition and scalar multiplication as
Then
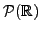 forms a real vector space.
forms a real vector space.
Suppose that
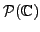 is the set of all polynomials with
complex coefficients, then with respect to the operations similar to what has
been defined above, the set
is the set of all polynomials with
complex coefficients, then with respect to the operations similar to what has
been defined above, the set
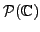 is a real vector space.
If we allow the scalars to be complex numbers then
is a real vector space.
If we allow the scalars to be complex numbers then
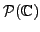 becomes
a complex vector space.
becomes
a complex vector space.
- Let
![$ C([-1,1])$](img1089.png) be the set of all
real valued continuous functions on the
interval
be the set of all
real valued continuous functions on the
interval ![$ [-1, 1].$](img1090.png) For
For
![$ f , g \in C([-1,1])$](img1091.png) and
and
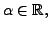 define
define
Then ![$ C([-1,1])$](img1089.png) forms a real vector space.
The operations defined above are called POINT WISE ADDITION AND
SCALAR MULTIPLICATION.
forms a real vector space.
The operations defined above are called POINT WISE ADDITION AND
SCALAR MULTIPLICATION.
- Let
 and
and 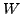 be real vector spaces with binary operations
be real vector spaces with binary operations
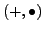 and
and
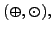 respectively.
Consider the
following operations on the set
respectively.
Consider the
following operations on the set
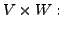 for
for
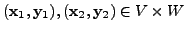 and
and
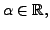 define
define
On the right hand side, we write
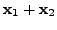 to mean the addition in
to mean the addition in 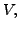 while
while
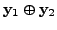 is the addition
in
is the addition
in 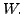 Similarly,
Similarly,
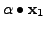 and
and
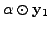 come from
scalar multiplication
in
come from
scalar multiplication
in  and
and 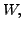 respectively. With the above definitions,
respectively. With the above definitions,
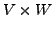 also
forms a real vector space.
also
forms a real vector space.
The readers are advised to justify the statements made in the above examples.
From now on, we will use `
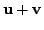 ' in place of `
' in place of `
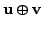 '
and `
'
and `
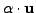 or
or
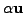 ' in place of `
' in place of `
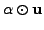 '.
'.
A K Lal
2007-09-12
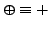 and
and
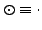 )
forms a vector space over
)
forms a vector space over
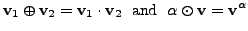
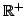 is a real vector space with
is a real vector space with 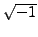 is denoted
is denoted 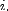
 matrices with complex entries.
Then
matrices with complex entries.
Then
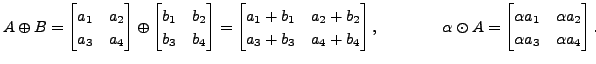
 with coefficients from
with coefficients from
 Hence, we can assume
Hence, we can assume
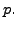 We
now define the vector addition and scalar multiplication as
We
now define the vector addition and scalar multiplication as
![]() is the set of all polynomials with
complex coefficients, then with respect to the operations similar to what has
been defined above, the set
is the set of all polynomials with
complex coefficients, then with respect to the operations similar to what has
been defined above, the set
![]() is a real vector space.
If we allow the scalars to be complex numbers then
is a real vector space.
If we allow the scalars to be complex numbers then
![]() becomes
a complex vector space.
becomes
a complex vector space.
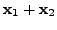 to mean the addition in
to mean the addition in 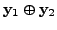 is the addition
in
is the addition
in 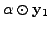 come from
scalar multiplication
in
come from
scalar multiplication
in 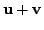 ' in place of `
' in place of `
![]() '
and `
'
and `
![]() or
or
![]() ' in place of `
' in place of `
![]() '.
'.