Next: Linear Combinations Up: Vector Spaces Previous: Examples Contents
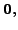
Hence
But if we think of ![]() as a subset of the real vector space
as a subset of the real vector space
![]() (component wise addition and scalar multiplication), then
(component wise addition and scalar multiplication), then ![]() is a subspace. Check that
is a subspace. Check that
![]() is a subspace of
is a subspace of ![]() (
(![]() represents a line passing through the point
represents a line passing through the point ![]() , the zero vector of
, the zero vector of ![]() ).
).
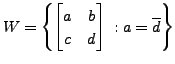 be a subset of
be a subset of
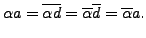
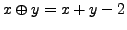 and the scalar multiplication by
and the scalar multiplication by
A K Lal 2007-09-12