Next: Linear Independence Up: Vector Spaces Previous: Subspaces Contents
For each vector, the LINEAR COMBINATION IN TERMS OF THE VECTORS
Check that
![]() Also, in this case, the vector
Also, in this case, the vector ![]() DOES NOT HAVE A
UNIQUE EXPRESSION AS LINEAR COMBINATION OF VECTORS
DOES NOT HAVE A
UNIQUE EXPRESSION AS LINEAR COMBINATION OF VECTORS
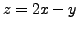 , take
, take
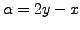 and
and
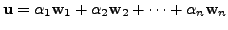 and
and
Thus,
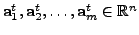 and
columns
and
columns
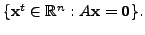
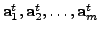 be the rows of
the matrix
be the rows of
the matrix 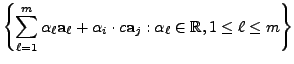 |
|||
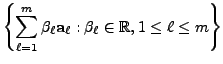 |
|||
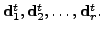 Then
Then
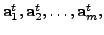 then
then
Hence the required result follows. height6pt width 6pt depth 0pt
![$\displaystyle \{f \in C([-1, 1]) : f'(\frac{1}{4}) {\mbox{exists }} \}.$](img1244.png) |
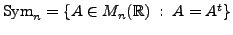
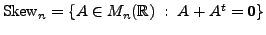
 and
and
A K Lal 2007-09-12