EXAMPLE 3.2.2
- Let
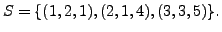 Then check that
Then check that
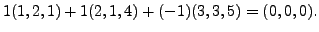 Since
Since
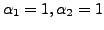 and
and
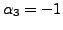 is a solution of
(3.2.1), so the set
is a solution of
(3.2.1), so the set 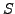 is a linearly dependent
subset of
is a linearly dependent
subset of
- Let
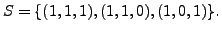 Suppose there exists
Suppose there exists
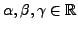 such that
such that
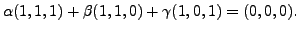 Then check that in this case we necessarily
have
Then check that in this case we necessarily
have
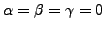 which shows that the set
which shows that the set
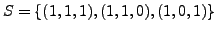 is a linearly independent subset of
is a linearly independent subset of
In other words, if
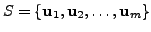 is a
non-empty subset of a vector space
is a
non-empty subset of a vector space 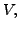 then to check whether the
set
then to check whether the
set 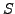 is linearly dependent or independent, one needs to
consider the equation
is linearly dependent or independent, one needs to
consider the equation
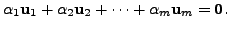 |
(3.2.1) |
In case
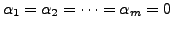 is THE ONLY
SOLUTION of (3.2.1), the set
is THE ONLY
SOLUTION of (3.2.1), the set 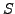 becomes a
linearly independent subset of
becomes a
linearly independent subset of 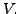 Otherwise, the set
Otherwise, the set 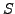 becomes a linearly dependent subset of
becomes a linearly dependent subset of 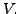
PROPOSITION 3.2.3
Let  be a vector space.
be a vector space.
- Then the zero-vector cannot
belong to a linearly independent set.
- If
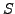 is a linearly independent subset of
is a linearly independent subset of 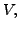 then every subset of
then every subset of 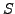 is also linearly independent.
is also linearly independent.
- If
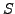 is a linearly dependent subset of
is a linearly dependent subset of  then every set containing
then every set containing 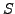 is also linearly dependent.
is also linearly dependent.
Proof.
We give the proof of the first part. The reader is
required to supply the proof of other parts.
Let
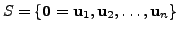
be a set consisting of the
zero vector. Then for any

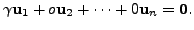
Hence, for the system
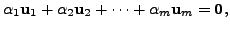
we have
a non-zero solution
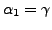
and
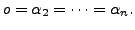
Therefore, the set
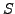
is linearly
dependent.
height6pt width 6pt depth 0pt
THEOREM 3.2.4
Let
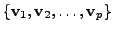 be a linearly independent subset
of a vector space
be a linearly independent subset
of a vector space 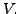 Suppose there exists a vector
Suppose there exists a vector
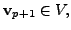 such that the set
such that the set
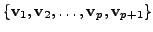 is
linearly dependent, then
is
linearly dependent, then
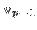 is a linear combination of
is a linear combination of
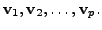
Proof.
Since the set
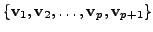
is linearly dependent, there exist scalars
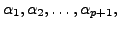 NOT ALL ZERO
NOT ALL ZERO such
that
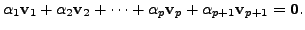 |
(3.2.2) |
C
LAIM:
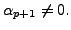
Let if
possible
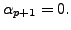
Then equation (
3.2.2)
gives
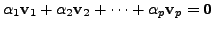
with not all
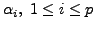
zero. Hence, by
the definition of linear independence, the set
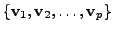
is linearly dependent which is contradictory
to our hypothesis. Thus,
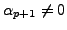
and we get
Note that
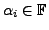
for every
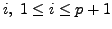
and hence
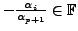
for
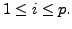
Hence the result follows.
height6pt width 6pt depth 0pt
We now state two important corollaries of the above theorem.
We don't give their proofs as they are easy consequence of the above
theorem.
COROLLARY 3.2.5
Let
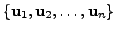 be a linearly dependent subset of a vector space
be a linearly dependent subset of a vector space 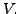 Then there
exists a smallest
Then there
exists a smallest
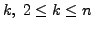 such that
such that
The next corollary follows immediately from Theorem 3.2.4
and Corollary 3.2.5.
COROLLARY 3.2.6
Let
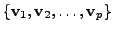 be a linearly independent subset
of a vector space
be a linearly independent subset
of a vector space 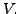 Suppose there exists a vector
Suppose there exists a vector
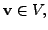 such that
such that
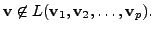 Then the set
Then the set
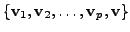 is also a linearly independent
subset of
is also a linearly independent
subset of 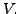
EXERCISE 3.2.7
- Consider the vector space
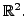 Let
Let
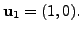 Find
all choices for the vector
Find
all choices for the vector
 such that the set
such that the set
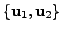 is linear independent subset of
is linear independent subset of
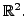 Does there exist
choices for vectors
Does there exist
choices for vectors
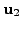 and
and
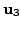 such that the set
such that the set
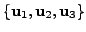 is linearly independent subset of
is linearly independent subset of
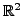 ?
?
- If
none of the elements appearing along the principal diagonal of a
lower triangular matrix is zero, show that the row vectors are
linearly independent in
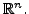 The same is true for column
vectors.
The same is true for column
vectors.
- Let
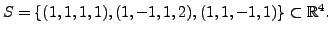 Determine whether or not the vector
Determine whether or not the vector
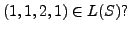
- Show that
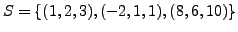 is linearly dependent in
is linearly dependent in
- Show that
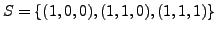 is a linearly independent set in
is a linearly independent set in
 In general if
In general if
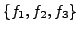 is a linearly
independent set then
is a linearly
independent set then
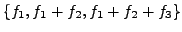 is
also a linearly independent set.
is
also a linearly independent set.
- In
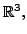 give
an example of
give
an example of 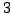 vectors
vectors
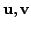 and
and
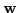 such that
such that
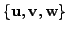 is linearly dependent but any set of
is linearly dependent but any set of 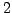 vectors from
vectors from
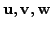 is linearly independent.
is linearly independent.
- What is the maximum number
of linearly independent vectors in
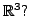
- Show
that any set of
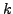 vectors in
vectors in
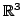 is linearly
dependent if
is linearly
dependent if 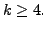
- Is the set of vectors
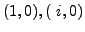 linearly independent subset of
linearly independent subset of
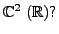
- Suppose
 is a collection of vectors such that
is a collection of vectors such that
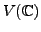 as well as
as well as
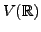 are vector spaces. Prove that the set
are vector spaces. Prove that the set
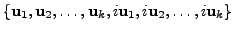 is a linearly independent subset of
is a linearly independent subset of
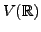 if and only if
if and only if
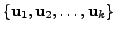 is a linear independent subset
of
is a linear independent subset
of
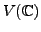 .
.
- Under
what conditions on
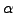 are the vectors
are the vectors
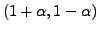 and
and
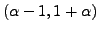 in
in
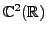 linearly
independent?
linearly
independent?
- Let
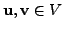 and
and 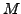 be a subspace of
be a subspace of
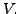 Further, let
Further, let 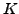 be the subspace spanned by
be the subspace spanned by 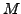 and
and
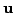 and
and
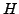 be the subspace spanned by
be the subspace spanned by 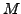 and
and
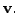 Show that if
Show that if
 and
and
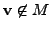 then
then
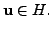
A K Lal
2007-09-12
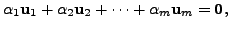
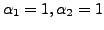 and
and
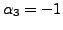 is a solution of
(3.2.1), so the set
is a solution of
(3.2.1), so the set ![]() is a
non-empty subset of a vector space
is a
non-empty subset of a vector space ![]() then to check whether the
set
then to check whether the
set ![]() is linearly dependent or independent, one needs to
consider the equation
is linearly dependent or independent, one needs to
consider the equation
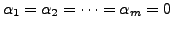 is THE ONLY
SOLUTION of (3.2.1), the set
is THE ONLY
SOLUTION of (3.2.1), the set 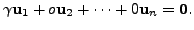 Hence, for the system
Hence, for the system
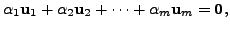 we have
a non-zero solution
we have
a non-zero solution
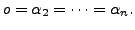 Therefore, the set
Therefore, the set 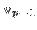 is a linear combination of
is a linear combination of
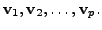
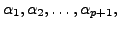 NOT ALL ZERO such
that
NOT ALL ZERO such
that
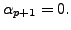 Then equation (3.2.2)
gives
Then equation (3.2.2)
gives
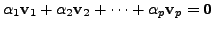 with not all
with not all
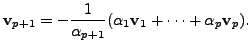
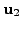 such that the set
such that the set
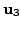 such that the set
such that the set