Next: Important Results Up: Finite Dimensional Vector Spaces Previous: Linear Independence Contents
Observe that if there
exists a
![]() such that
such that
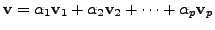 and
and
![]() then
then
But then the set
By convention, the linear span of an empty set is
![]() Hence,
the empty set is a basis of the vector space
Hence,
the empty set is a basis of the vector space
![]()
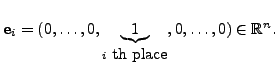 Then, the set
Then, the set
That is, if 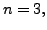 then the set
then the set
![]() forms an standard basis of
forms an standard basis of
![]()
Then by Remark 3.3.2,
A basis of ![]() can be obtained by the following method:
can be obtained by the following method:
The condition
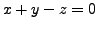 is equivalent to
is equivalent to
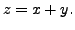 we replace the value of
we replace the value of ![]() with
with ![]() to get
to get
Hence,
Observe that ![]() is a vector in
is a vector in
![]() Also,
Also,
![]() and hence
and hence
![]() is not defined.
is not defined.
This basis has infinite number of vectors as the degree of the polynomial can be any positive integer.
In Example 3.3.3, the vector space of all polynomials is an example of an infinite dimensional vector space. All the other vector spaces are finite dimensional.
In the second case,
![]() . So, we choose a vector, say,
. So, we choose a vector, say,
![]() such that
such that
![]() Therefore, by Corollary 3.2.6, the set
Therefore, by Corollary 3.2.6, the set
![]() is linearly independent.
is linearly independent.
This process will finally end as ![]() is a finite dimensional vector space.
is a finite dimensional vector space.