Next: Ordered Bases Up: Bases Previous: Bases Contents
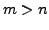 then this set is linearly dependent.
then this set is linearly dependent.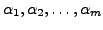 as the
as the
As
![]() is a basis of
is a basis of ![]() and
and
![]() for each
for each
![]() there exist scalars
there exist scalars
![]() such that
such that
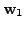 |
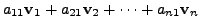 |
||
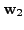 |
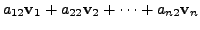 |
||
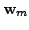 |
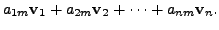 |
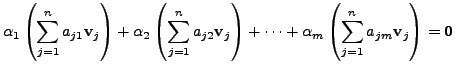 |
|||
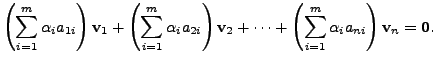 |
Since the set
![]() is linearly
independent, we have
is linearly
independent, we have
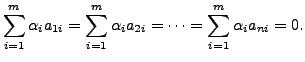
Therefore, finding
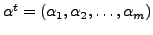 and
and
 Since
Since 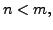 i.e.,
THE NUMBER OF EQUATIONS is strictly less than
THE NUMBER OF UNKNOWNS, Corollary 2.5.3
implies that the solution set consists of infinite number of
elements. Therefore, the equation (3.3.1) has a solution
with not all
i.e.,
THE NUMBER OF EQUATIONS is strictly less than
THE NUMBER OF UNKNOWNS, Corollary 2.5.3
implies that the solution set consists of infinite number of
elements. Therefore, the equation (3.3.1) has a solution
with not all
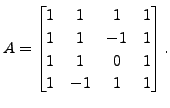 Applying row-reduction to
Applying row-reduction to 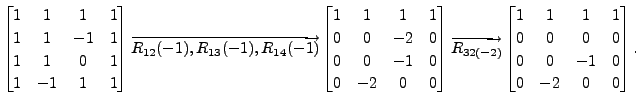
Observe that at the last step, in place of the elementary row operation
![]() ,
we can apply
,
we can apply
![]() to make the third row as the zero-row. In this case,
we get
to make the third row as the zero-row. In this case,
we get
![]() as a basis of
as a basis of ![]() .
.
So,
Hence, the set
For
![]() consider the functions
consider the functions
Then it can be easily verified that the set
The next theorem follows directly from Corollary 3.2.6 and Theorem 3.3.7. Hence, the proof is omitted.
Theorem 3.3.15 is equivalent to the following statement:
Let ![]() be a vector space of dimension
be a vector space of dimension ![]() Suppose,
we have found a linearly independent set
Suppose,
we have found a linearly independent set
[4]
![]() Then there exist vectors
Then there exist vectors
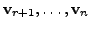 in
in ![]() such that
such that
![]() is a basis of
is a basis of
![]()
is given by
Thus, a basis of
To find a basis of
Now use Remark 3.3.8 to get the required basis.
Heuristically, we can also find the basis in the following way:
A vector of ![]() has the form
has the form
![]() for
for
![]() Substituting
Substituting ![]() and
and ![]() in
in
![]() gives us the
vector
gives us the
vector
![]() It can be easily verified that a basis of
It can be easily verified that a basis of ![]() is
is
Similarly, a vector of
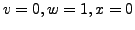 and
and 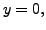 gives a vector
gives a vector
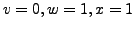 and
and
Recall that for two vector subspaces ![]() and
and ![]() of a vector space
of a vector space
![]() the vector subspace
the vector subspace ![]() (see Exercise 3.1.18.7)
is defined by
(see Exercise 3.1.18.7)
is defined by
With this definition, we have the following very important theorem (for a proof, see Appendix 14.4.1).
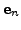 defined by
defined by
Now for different values of
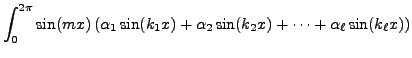 dx
dxto get the required result.]
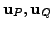 such that
such that
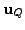 are unique?
are unique?
a subspace of
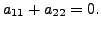 Show that
Show that  and
and
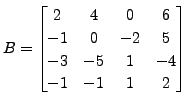 be two matrices. For
be two matrices. For 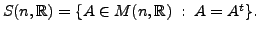
Before going to the next section, we prove that for any matrix
![]() of order
of order
![]()
Hence, there exists vectors
with
Therefore, there exist real numbers
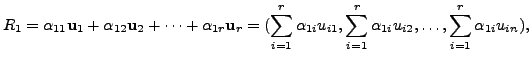
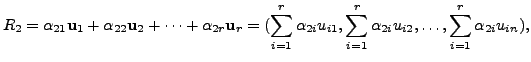
and so on, till
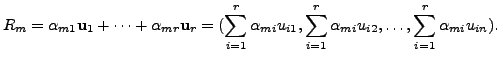
So,
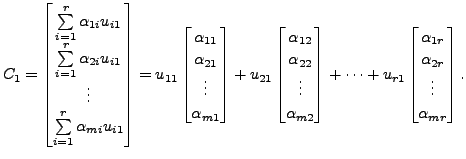
In general, for
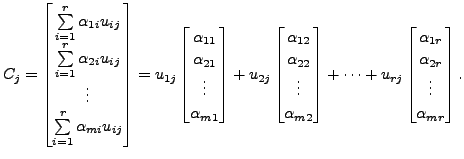
Therefore, we observe that the columns
Therefore,
A similar argument gives
Thus, we have the required result. height6pt width 6pt depth 0pt
A K Lal 2007-09-12