Next: Equivalent conditions for Invertibility Up: Existence of Solution of Previous: Example Contents
where
The following corollary of Theorem 2.5.1
is a very important result about the homogeneous linear system
![]()
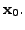 That is,
That is,
Also
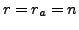 (see Theorem 2.5.1), we get
(see Theorem 2.5.1), we get
Now, let us assume that rank![]() Then
Then
So, by Theorem 2.5.1, the solution set of the linear system
We now state another important result whose proof is immediate from Theorem 2.5.1 and Corollary 2.5.3.
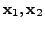 are two solutions of
are two solutions of
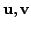 are two solutions of
are two solutions of
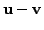 is
a solution of the system
is
a solution of the system
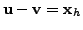 for
some solution
for
some solution
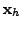 of
of
In conclusion, for
![]() the set of solutions of the system
the set of solutions of the system
![]() is of the form,
is of the form,
![]() where
where
![]() is a particular solution
of
is a particular solution
of
![]() and
and
![]() is a solution
is a solution
![]()
is consistent.
A K Lal 2007-09-12