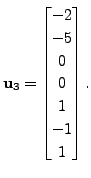Consider a linear system
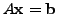 which after
the application of the Gauss-Jordan method
reduces to a matrix
which after
the application of the Gauss-Jordan method
reduces to a matrix
![$ [C \; \; {\mathbf d}]$](img479.png) with
with
For this particular
matrix
![$ [C \;\; {\mathbf d}],$](img626.png) we want to see the set of solutions.
We start with some observations.
we want to see the set of solutions.
We start with some observations.
Observations:
- The number of non-zero rows in
 is
is  This number is also
equal to the number of non-zero rows in
This number is also
equal to the number of non-zero rows in
![$ [C \;\; {\mathbf d}].$](img628.png)
- The first non-zero entry in the non-zero rows appear in columns
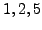 and
and 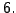
- Thus, the respective variables
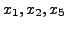 and
and 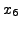 are the basic variables.
are the basic variables.
- The remaining variables,
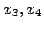 and
and 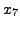 are free variables.
are free variables.
- We assign arbitrary constants
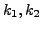 and
and 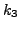 to
the free variables
to
the free variables 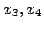 and
and 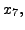 respectively.
respectively.
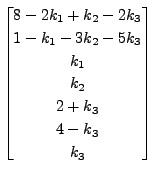
Hence, we have the set of solutions as
where 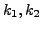 and
and 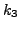 are arbitrary.
are arbitrary.
Let
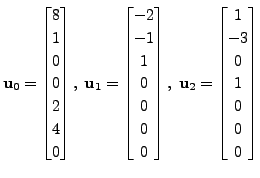 and
and
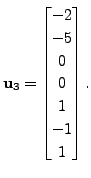
Then it can easily be verified that
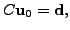 and for
and for
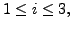
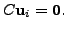
A similar idea is used in the proof of the next theorem and is omitted.
The interested readers can read the proof in Appendix
14.1.
A K Lal
2007-09-12
![$\displaystyle [C \;\; {\mathbf d}] = \begin{bmatrix}1 & 0 & 2 & -1 & 0 & 0 & 2 ...
...\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0
& 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{bmatrix}.$](img625.png)
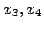 and
and 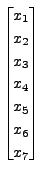
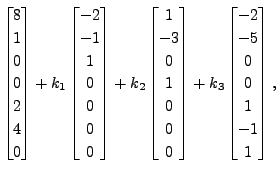
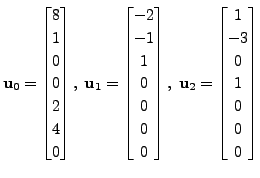 and
and