Next: Inverse and the Gauss-Jordan Up: Existence of Solution of Previous: Main Theorem Contents
Let if possible rank
![]() Then there exists an
invertible matrix
Then there exists an
invertible matrix ![]() (a product of elementary matrices)
such that
(a product of elementary matrices)
such that
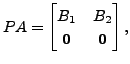 where
where ![]() is an
is an
![]() matrix. Since
matrix. Since ![]() is invertible, let
is invertible, let
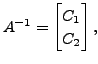 where
where ![]() is an
is an
![]() matrix. Then
matrix. Then
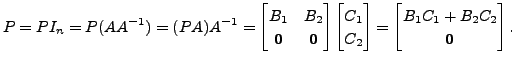 |
(2.5.1) |
Suppose ![]() is of full rank. This implies, the row reduced echelon form of
is of full rank. This implies, the row reduced echelon form of
![]() has all non-zero rows. But
has all non-zero rows. But ![]() has as many columns as rows and
therefore, the last row of the row reduced echelon form of
has as many columns as rows and
therefore, the last row of the row reduced echelon form of ![]() will be
will be
![]() Hence, the row reduced echelon form of
Hence, the row reduced echelon form of ![]() is the identity matrix.
is the identity matrix.
Since ![]() is row-equivalent to the identity
matrix there exist elementary matrices
is row-equivalent to the identity
matrix there exist elementary matrices
![]() such that
such that
![]() That is,
That is,
![]() is product of elementary matrices.
is product of elementary matrices.
Suppose
![]() where the
where the ![]() 's are elementary matrices.
We know that elementary matrices are invertible and product
of invertible matrices is also invertible, we get the
required result. height6pt width 6pt depth 0pt
's are elementary matrices.
We know that elementary matrices are invertible and product
of invertible matrices is also invertible, we get the
required result. height6pt width 6pt depth 0pt
The ideas of Theorem 2.5.8 will be used in the next subsection to find the inverse of an invertible matrix. The idea used in the proof of the first part also gives the following important Theorem. We repeat the proof for the sake of clarity.
Let if possible, rank
![]() Then there exists an
invertible matrix
Then there exists an
invertible matrix ![]() (a product of elementary matrices)
such that
(a product of elementary matrices)
such that
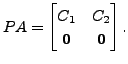 Let
Let
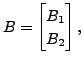 where
where ![]() is an
is an
![]() matrix. Then
matrix. Then
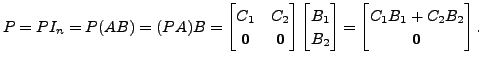 |
(2.5.2) |
Using the first part, it is clear that the matrix ![]() in the second part,
is invertible. Hence
in the second part,
is invertible. Hence
Thus,
Since ![]() is invertible, by Theorem 2.5.8
is invertible, by Theorem 2.5.8 ![]() is of full rank. That is, for the linear system
is of full rank. That is, for the linear system
![]() the number of unknowns is equal to the rank of the matrix
the number of unknowns is equal to the rank of the matrix ![]() Hence, by Theorem 2.5.1 the system
Hence, by Theorem 2.5.1 the system
![]() has a unique solution
has a unique solution
![]()
Let if possible ![]() be non-invertible.
Then by Theorem 2.5.8, the matrix
be non-invertible.
Then by Theorem 2.5.8, the matrix ![]() is not of full
rank. Thus by Corollary 2.5.3, the linear system
is not of full
rank. Thus by Corollary 2.5.3, the linear system
![]() has infinite number of solutions. This
contradicts the assumption that
has infinite number of solutions. This
contradicts the assumption that
![]() has only
the trivial solution
has only
the trivial solution
![]()
Since ![]() is invertible, for every
is invertible, for every
![]() the system
the system
![]() has a unique solution
has a unique solution
![]()
For
![]() define
define
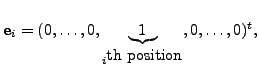 and consider the linear system
and consider the linear system
![]() By assumption, this system has a solution
By assumption, this system has a solution
![]() for each
for each
![]() Define a matrix
Define a matrix
![]() That is, the
That is, the
![]() column of
column of ![]() is the solution of the system
is the solution of the system
![]() Then
Then
Therefore, by Theorem 2.5.9, the matrix
A K Lal 2007-09-12