Next: Determinant Up: Existence of Solution of Previous: Equivalent conditions for Invertibility Contents
We first give a consequence of Theorem 2.5.8 and then use it to find the inverse of an invertible matrix.
Summary: Let ![]() be an
be an
![]() matrix. Apply the
Gauss-Jordan method to the matrix
matrix. Apply the
Gauss-Jordan method to the matrix
![]() Suppose the row reduced echelon form of the matrix
Suppose the row reduced echelon form of the matrix
![]() is
is
![]() If
If ![]() then
then
![]() or else
or else
![]() is not invertible.
is not invertible.
 using the Gauss-Jordan method.
using the Gauss-Jordan method.
Solution: Consider the matrix
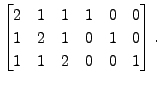 A sequence of steps in the Gauss-Jordan
method are:
A sequence of steps in the Gauss-Jordan
method are:
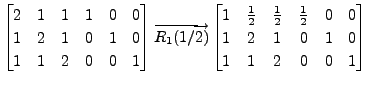
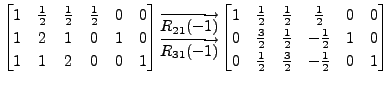
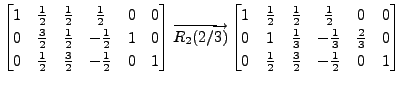
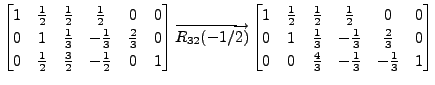
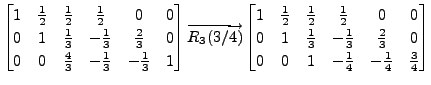
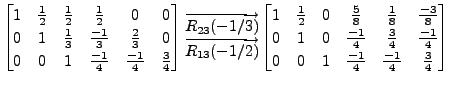
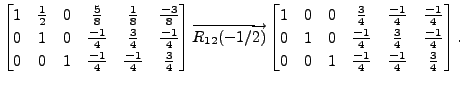
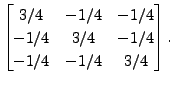
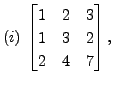
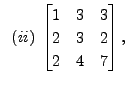
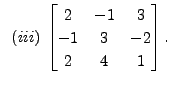
A K Lal 2007-09-12