Next: Adjoint of a Matrix Up: Linear System of Equations Previous: Inverse and the Gauss-Jordan Contents
Notation: For an
![]() matrix
matrix ![]() by
by
![]() we mean the submatrix
we mean the submatrix ![]() of
of ![]() which is obtained
by deleting the
which is obtained
by deleting the
![]() row and
row and
![]() column.
column.
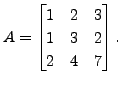 Then
Then
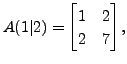
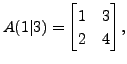 and
and
![\begin{displaymath}\det(A) = \left \{
\begin{array}{lc} a & {\mbox{if }} A = [a]...
...l(A(1\vert j)\bigr), & {\mbox{
otherwise}}.
\end{array} \right.\end{displaymath}](img759.png)

The proof of the next theorem is omitted. The interested reader is advised to go through Appendix 14.3.
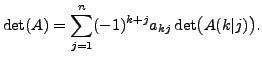
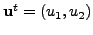 and
and
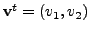 be two vectors in
be two vectors in
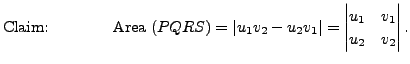
Recall that the dot product,
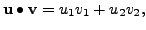 and
and
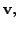 then
then
Which tells us,
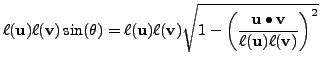 |
|||
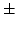 times
the area of the parallelogram.
times
the area of the parallelogram.
Note here that if
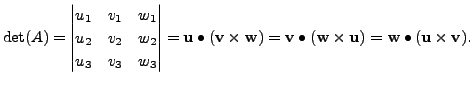
Let
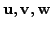 as adjacent vertices. Then
observe that
as adjacent vertices. Then
observe that
Hence,
![]()
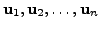 as adjacent vertices:
as adjacent vertices:
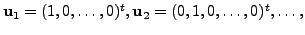 and
and
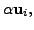 for some
for some
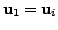 for some
for some
In general, for any
![]() matrix
matrix ![]() it can be proved that
it can be proved that
![]() is indeed equal to the volume of the
is indeed equal to the volume of the ![]() -dimensional
parallelopiped. The actual proof is beyond the scope of this book.
-dimensional
parallelopiped. The actual proof is beyond the scope of this book.