Next: Cramer's Rule Up: Determinant Previous: Determinant Contents
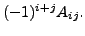
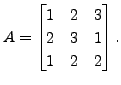 Then
Then
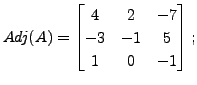
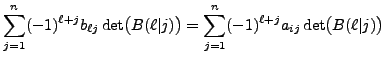 |
|||
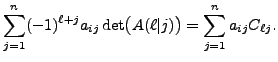 |
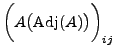 |
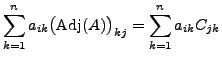 |
||
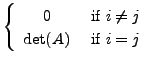 |
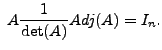 Therefore,
Therefore,
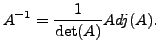
height6pt width 6pt depth 0pt
The next corollary is an easy consequence of Theorem 2.6.12 (recall Theorem 2.5.9).
Step 2. Suppose
![]()
Then ![]() is not invertible.
Hence, there exists an invertible matrix
is not invertible.
Hence, there exists an invertible matrix ![]() such that
such that
![]() where
where
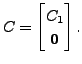 So,
So,
![]() and therefore
and therefore
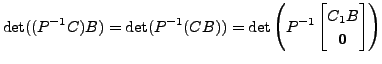 |
|||
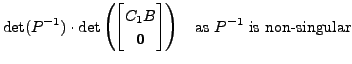 |
|||
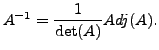 Thus,
Thus,
Suppose ![]() has an inverse. Then there exists a matrix
has an inverse. Then there exists a matrix ![]() such that
such that
![]() Taking determinant of both sides, we get
Taking determinant of both sides, we get
This implies that
If ![]() is singular, then
is singular, then
![]() Hence,
by Corollary 2.6.16,
Hence,
by Corollary 2.6.16, ![]() doesn't have an inverse.
Therefore,
doesn't have an inverse.
Therefore, ![]() also doesn't have an inverse
(for if
also doesn't have an inverse
(for if ![]() has an inverse then
has an inverse then
![]() Thus again by Corollary 2.6.16,
Thus again by Corollary 2.6.16,
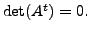 Therefore, we again have
Therefore, we again have
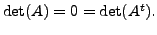
Hence, we have
![]() height6pt width 6pt depth 0pt
height6pt width 6pt depth 0pt
A K Lal 2007-09-12