Next: Miscellaneous Exercises Up: Determinant Previous: Adjoint of a Matrix Contents
Recall the following:
The following theorem gives a direct method of finding the
solution of the linear system
![]() when
when
![]()
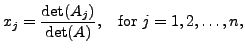
where
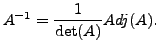 Thus, the linear
system
Thus, the linear
system
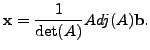 Hence,
Hence,
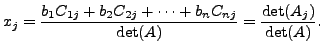
height6pt width 6pt depth 0pt
The theorem implies that
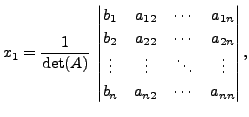
and in general
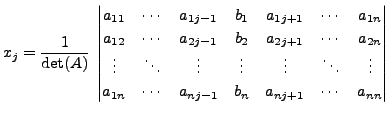
for
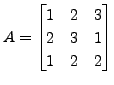 and
and
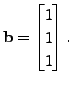 Use Cramer's rule to find a vector
Use Cramer's rule to find a vector
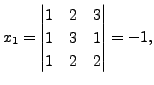
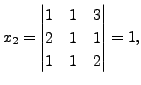 and
and
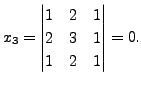 That is,
That is,
A K Lal 2007-09-12