Next: Dimension of Up: Appendix Previous: Determinant Contents
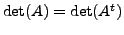 , where recall that
, where recall that 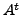 is the transpose of the matrix
is the transpose of the matrix
Let
![]() be a transposition. Then by Proposition 14.2.4,
be a transposition. Then by Proposition 14.2.4,
![]() . Hence by the definition of determinant
and Example 14.2.14.2,
we have
. Hence by the definition of determinant
and Example 14.2.14.2,
we have
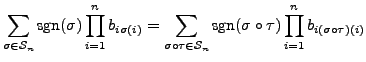 |
|||
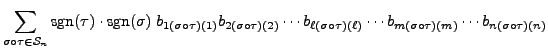 |
|||
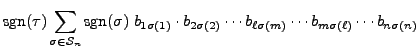 |
|||
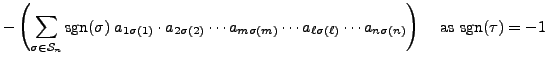 |
|||
Proof of Part 2. Suppose that
![]() is obtained by multiplying the
is obtained by multiplying the
![]() row of
row of ![]() by
by ![]() . Then
. Then
![]() and
and
![]() for
for
![]() .
Then
.
Then
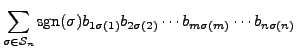 |
|||
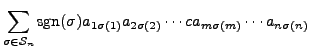 |
|||
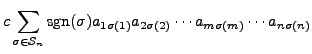 |
|||
Proof of Part 3. Note that
![]() . So, each term in the expression for determinant, contains one
entry from each row. Hence, from the condition that
. So, each term in the expression for determinant, contains one
entry from each row. Hence, from the condition that ![]() has a row consisting of all zeros, the value of
each term is 0
. Thus,
has a row consisting of all zeros, the value of
each term is 0
. Thus,
![]() .
.
Proof of Part 4. Suppose that the
![]() and
and
![]() row of
row of ![]() are equal. Let
are equal. Let ![]() be the matrix obtained from
be the matrix obtained from ![]() by interchanging the
by interchanging the
![]() and
and
![]() rows. Then
by the first part,
rows. Then
by the first part,
![]() But the assumption implies that
But the assumption implies that ![]() . Hence,
. Hence,
![]() .
So, we have
.
So, we have
![]() Hence,
Hence,
![]() .
.
Proof of Part 5. By definition and the given assumption, we have
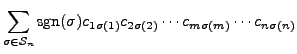 |
|||
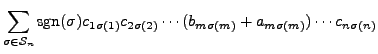 |
|||
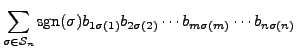 |
|||
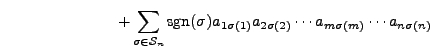 |
|||
Proof of Part 6. Suppose that
![]() is obtained from
is obtained from ![]() by
replacing the
by
replacing the ![]() th row by itself plus
th row by itself plus ![]() times the
times the ![]() th row, for
th row, for
![]() .
Then
.
Then
![]() and
and
![]() for
for
![]() .
Then
.
Then
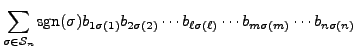 |
|||
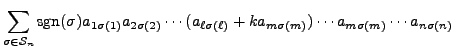 |
|||
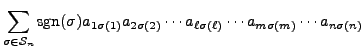 |
|||
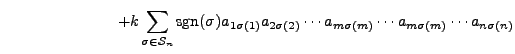 |
|||
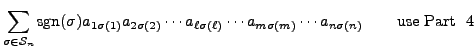 |
|||
Proof of Part 7. First let us assume that ![]() is an upper triangular matrix.
Observe that if
is an upper triangular matrix.
Observe that if
![]() is different from the identity permutation
then
is different from the identity permutation
then
![]() . So, for every
. So, for every
![]() ,
there exists a positive integer
,
there exists a positive integer
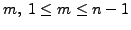 (depending on
(depending on ![]() )
such that
)
such that
![]() . As
. As ![]() is an upper triangular matrix,
is an upper triangular matrix,
![]() for each
for each
![]() . Hence the result follows.
. Hence the result follows.
A similar reasoning holds true, in case ![]() is a lower triangular matrix.
is a lower triangular matrix.
Proof of Part 8. Let ![]() be the identity matrix of order
be the identity matrix of order ![]() .
Then using Part 7,
.
Then using Part 7,
![]() .
Also, recalling the notations for the elementary matrices given in
Remark 2.3.14, we have
.
Also, recalling the notations for the elementary matrices given in
Remark 2.3.14, we have
![]() (using Part 1)
(using Part 1)
![]() (using Part 2) and
(using Part 2) and
![]() (using Part 6).
Again using Parts 1, 2 and 6, we get
(using Part 6).
Again using Parts 1, 2 and 6, we get
![]() .
.
Proof of Part 9. Suppose ![]() is invertible. Then by Theorem 2.5.8,
is invertible. Then by Theorem 2.5.8,
![]() is a product of elementary matrices. That is, there exist elementary matrices
is a product of elementary matrices. That is, there exist elementary matrices
![]() such that
such that
![]() . Now a repeated application of Part 8 implies that
. Now a repeated application of Part 8 implies that
![]() . But
. But
![]() for
for
![]() . Hence,
. Hence,
![]() .
.
Now assume that
![]() . We show that
. We show that ![]() is invertible. On the contrary, assume that
is invertible. On the contrary, assume that ![]() is not invertible.
Then by Theorem 2.5.8, the matrix
is not invertible.
Then by Theorem 2.5.8, the matrix ![]() is not of full rank. That is there exists a positive integer
is not of full rank. That is there exists a positive integer 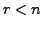 such that
such that
![]() . So, there exist elementary matrices
. So, there exist elementary matrices
![]() such that
such that
![$ E_1 E_2 \cdots E_k A = \left[\begin{array}{c} B \\ {\mathbf 0}\end{array}\right]$](img5920.png) .
Therefore, by Part 3 and a repeated application of Part 8,
.
Therefore, by Part 3 and a repeated application of Part 8,
![$\displaystyle \det(E_1) \det(E_2) \cdots \det(E_k) \det(A) = \det(E_1 E_2 \cdot...
...et \left( \left[\begin{array}{c} B \\ {\mathbf 0}\end{array}\right] \right)= 0.$](img5921.png)
But
Proof of Part 10. Suppose ![]() is not invertible. Then by Part 9,
is not invertible. Then by Part 9,
![]() . Also, the product matrix
. Also, the product matrix ![]() is also not invertible. So,
again by Part 9,
is also not invertible. So,
again by Part 9,
![]() . Thus,
. Thus,
![]() .
.
Now suppose that ![]() is invertible. Then by Theorem 2.5.8,
is invertible. Then by Theorem 2.5.8,
![]() is a product of elementary matrices. That is, there exist elementary matrices
is a product of elementary matrices. That is, there exist elementary matrices
![]() such that
such that
![]() . Now a repeated application of Part 8 implies that
. Now a repeated application of Part 8 implies that
Proof of Part 11. Let
![]() . Then
. Then
![]() for
for
![]() .
By Proposition 14.2.4, we know that
.
By Proposition 14.2.4, we know that
![]() . Also
. Also
![]() .
Hence,
.
Hence,
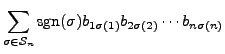 |
|||
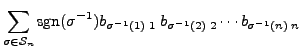 |
|||
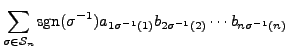 |
|||
height6pt width 6pt depth 0pt
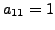 and
and
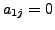 for
for
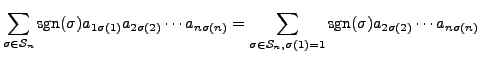 |
|||
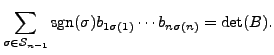 |
We are now ready to relate this definition of determinant with the one given in Definition 2.6.2.
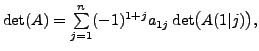 where recall that
where recall that 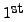 row and the
row and the
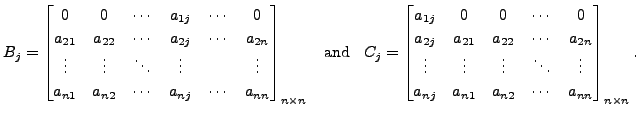
Then by Theorem 14.3.1.5,
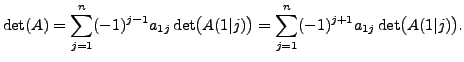
height6pt width 6pt depth 0pt
A K Lal 2007-09-12