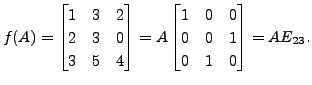DEFINITION 2.3.13
A square matrix 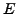 of order
of order 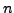 is called an elementary
matrix if it is obtained by applying exactly one elementary row
operation to the identity matrix,
is called an elementary
matrix if it is obtained by applying exactly one elementary row
operation to the identity matrix, 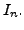
Remark 2.3.14
There are three types of elementary matrices.
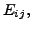 which is obtained by the application of the
elementary row operation
which is obtained by the application of the
elementary row operation 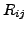 to the identity matrix,
to the identity matrix, 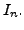 Thus, the
Thus, the
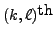 entry of
entry of 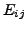 is
is
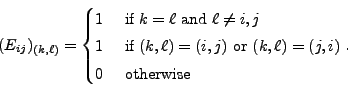
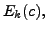 which is
obtained by the application of the elementary row operation
which is
obtained by the application of the elementary row operation
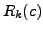 to the identity matrix,
to the identity matrix, 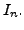 The
The
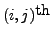 entry of
entry of 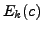 is
is
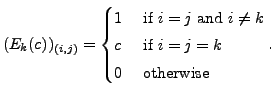
-
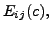 which is obtained by the application of the
elementary row operation
which is obtained by the application of the
elementary row operation 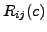 to the identity matrix,
to the identity matrix,
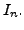 The
The
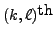 entry of
entry of 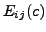 is
is
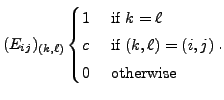
In particular, if we start with a
 identity matrix
identity matrix 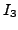 , then
, then
EXAMPLE 2.3.15
- Let
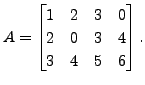 Then
Then
That is, interchanging the two rows of the matrix  is same as
multiplying on the left by the corresponding elementary matrix. In
other words, we see that the left multiplication of elementary
matrices to a matrix results in elementary row operations.
is same as
multiplying on the left by the corresponding elementary matrix. In
other words, we see that the left multiplication of elementary
matrices to a matrix results in elementary row operations.
- Consider the augmented matrix
![$ [A \; {\mathbf b}] = \begin{bmatrix}0 & 1 & 1 & 2 \\
2 & 0 & 3 & 5 \\ 1 & 1 & 1 & 3 \end{bmatrix}.$](img537.png) Then the result of the
steps given below is same as the matrix product
Then the result of the
steps given below is same as the matrix product
Now, consider an
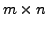 matrix
matrix  and an elementary matrix
and an elementary matrix
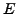 of order
of order 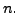 Then multiplying by
Then multiplying by 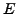 on the right to
on the right to  corresponds
to applying column transformation on the matrix
corresponds
to applying column transformation on the matrix 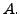 Therefore, for each
elementary matrix, there is a corresponding column
transformation. We summarize:
Therefore, for each
elementary matrix, there is a corresponding column
transformation. We summarize:
DEFINITION 2.3.16
The column transformations obtained by right
multiplication of elementary matrices are
called elementary column operations.
EXAMPLE 2.3.17
Let
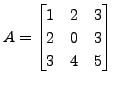 and consider the elementary column operation
and consider the elementary column operation
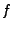 which interchanges
the second and the third column of
which interchanges
the second and the third column of 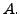 Then
Then
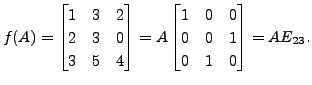
EXERCISE 2.3.18
- Let
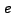 be an elementary row operation and let
be an elementary row operation and let
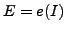 be the corresponding elementary matrix.
That is,
be the corresponding elementary matrix.
That is, 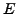 is the matrix obtained from
is the matrix obtained from 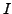 by applying
the elementary row operation
by applying
the elementary row operation 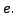 Show that
Show that
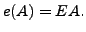
- Show that the Gauss elimination method is same as
multiplying by a series of elementary matrices on the left
to the augmented matrix. Does the Gauss-Jordan method also corresponds to multiplying by elementary
matrices on the left? Give reasons.
- Let
 and
and 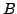 be two
be two
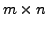 matrices. Then prove that the two matrices
matrices. Then prove that the two matrices 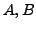 are
row-equivalent if and only if
are
row-equivalent if and only if 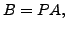 where
where  is product of
elementary matrices. When is this
is product of
elementary matrices. When is this  unique?
unique?
- Show that every elementary matrix is
invertible. Is the inverse of an elementary matrix,
also an elementary matrix?
A K Lal
2007-09-12
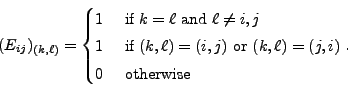
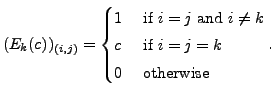
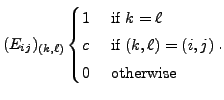
![]() identity matrix
identity matrix ![]() , then
, then
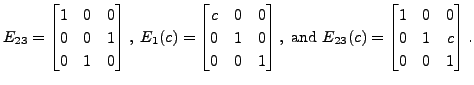
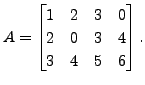 Then
Then
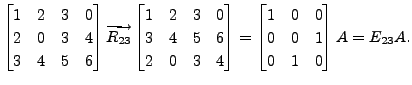
![$ [A \; {\mathbf b}] = \begin{bmatrix}0 & 1 & 1 & 2 \\
2 & 0 & 3 & 5 \\ 1 & 1 & 1 & 3 \end{bmatrix}.$](img537.png) Then the result of the
steps given below is same as the matrix product
Then the result of the
steps given below is same as the matrix product 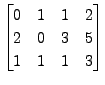
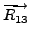
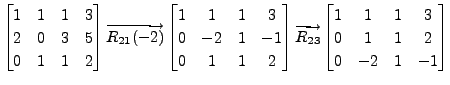
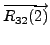
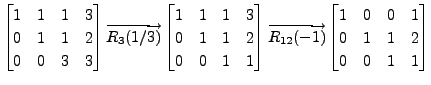
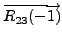
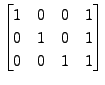
![]() matrix
matrix ![]() and an elementary matrix
and an elementary matrix
![]() of order
of order ![]() Then multiplying by
Then multiplying by ![]() on the right to
on the right to ![]() corresponds
to applying column transformation on the matrix
corresponds
to applying column transformation on the matrix ![]() Therefore, for each
elementary matrix, there is a corresponding column
transformation. We summarize:
Therefore, for each
elementary matrix, there is a corresponding column
transformation. We summarize:
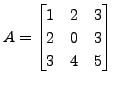 and consider the elementary column operation
and consider the elementary column operation