DEFINITION 2.3.1 (Row Reduced Form of a Matrix)
A matrix 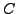 is said to be in the row reduced form if
is said to be in the row reduced form if
- THE FIRST NON-ZERO ENTRY IN EACH ROW OF
MATHEND000# IS
MATHEND000#
- THE COLUMN CONTAINING THIS
MATHEND000# HAS ALL ITS OTHER ENTRIES ZERO.
A matrix in the row reduced form is also called a ROW REDUCED MATRIX.
DEFINITION 2.3.3 (Leading Term, Leading Column)
For a row-reduced matrix, the first non-zero entry of any row
is called a LEADING TERM. The columns containing the
leading terms are called the LEADING COLUMNS.
DEFINITION 2.3.4 (Basic, Free Variables)
Consider the linear system
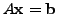 in
in 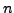 variables and
variables and 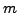 equations. Let
equations. Let
![$ [C \; \; {\mathbf d}]$](img479.png) be the row-reduced matrix obtained by applying the Gauss elimination
method to the augmented matrix
be the row-reduced matrix obtained by applying the Gauss elimination
method to the augmented matrix
![$ [ A \; \; {\mathbf b}].$](img424.png) Then the variables corresponding to
the leading columns in the first
Then the variables corresponding to
the leading columns in the first 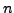 columns of
columns of
![$ [C \; \; {\mathbf d}]$](img479.png) are called the BASIC variables. The variables which are not basic are called
FREE variables.
are called the BASIC variables. The variables which are not basic are called
FREE variables.
The free variables are called so as they can be assigned arbitrary
values and the value of the basic variables can then be written in
terms of the free variables.
Observation: In Example 2.2.12,
the solution set was given by
That is, we had two basic variables, 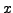 and
and 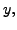 and
and 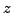 as a free variable.
as a free variable.
Remark 2.3.5
It is very important to
observe that if there are 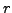 non-zero rows in the
row-reduced form of the matrix then there will be
non-zero rows in the
row-reduced form of the matrix then there will be 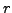 leading
terms. That is, there will be
leading
terms. That is, there will be 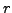 leading columns. Therefore,
IF THERE ARE
MATHEND000# LEADING TERMS AND
MATHEND000# VARIABLES,
THEN THERE WILL BE
MATHEND000# BASIC VARIABLES AND
MATHEND000# FREE VARIABLES.
leading columns. Therefore,
IF THERE ARE
MATHEND000# LEADING TERMS AND
MATHEND000# VARIABLES,
THEN THERE WILL BE
MATHEND000# BASIC VARIABLES AND
MATHEND000# FREE VARIABLES.
Subsections
A K Lal
2007-09-12
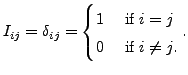
 and
and
 are also in row reduced form.
are also in row reduced form.
 is not in the row reduced form. (why?)
is not in the row reduced form. (why?)