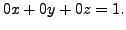DEFINITION 2.2.10 (Forward/Gauss Elimination Method)
Gaussian elimination is a method of solving a linear system
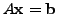 (consisting of
(consisting of 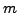 equations in
equations in 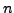 unknowns)
by bringing the augmented matrix
unknowns)
by bringing the augmented matrix
to an upper triangular form
This elimination process is also called the forward elimination method.
The following examples illustrate the Gauss elimination procedure.
Solution: In this case, the augmented matrix is
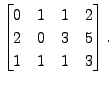 The method proceeds along the
following steps.
The method proceeds along the
following steps.
- Interchange
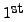 and
and
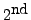 equation (or
equation (or  ).
).
- Divide the
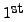 equation by
equation by 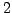 (or
(or 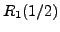 ).
).
- Add
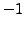 times the
times the
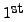 equation to the
equation to the
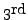 equation
(or
equation
(or
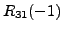 ).
).
- Add
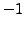 times the
times the
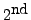 equation to the
equation to the
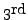 equation (or
equation (or
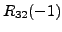 ).
).
- Multiply the
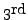 equation by
equation by
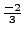 (or
(or
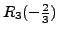 ).
).
The last equation gives 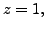 the second equation now gives
the second equation now gives 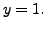 Finally the first equation gives
Finally the first equation gives 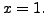 Hence the set of
solutions is
Hence the set of
solutions is
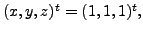 A UNIQUE
SOLUTION.
A UNIQUE
SOLUTION.
Solution: In this case, the augmented matrix is
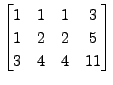 and the method proceeds as follows:
and the method proceeds as follows:
- Add
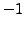 times the first equation to the second equation.
times the first equation to the second equation.
- Add
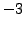 times the first equation to the third equation.
times the first equation to the third equation.
- Add
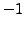 times the second equation to the third equation
times the second equation to the third equation
Thus, the set of solutions is
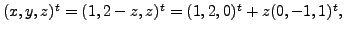 with
with 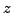 arbitrary. In other words, the system has INFINITE NUMBER
OF SOLUTIONS.
arbitrary. In other words, the system has INFINITE NUMBER
OF SOLUTIONS.
Solution: In this case, the augmented matrix is
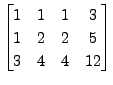 and the method proceeds as follows:
and the method proceeds as follows:
- Add
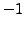 times the first equation to the second equation.
times the first equation to the second equation.
- Add
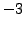 times the first equation to the third equation.
times the first equation to the third equation.
- Add
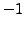 times the second equation to the third equation
times the second equation to the third equation
The third equation in the last step is
This can never hold for any value of 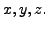 Hence, the
system has NO SOLUTION.
Hence, the
system has NO SOLUTION.
Remark 2.2.14
Note that to solve a linear system,
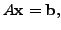 one needs to
apply only the elementary
row operations to the augmented matrix
one needs to
apply only the elementary
row operations to the augmented matrix
![$ [ A \; \; {\mathbf b}].$](img424.png)
A K Lal
2007-09-12
![$\displaystyle [A \;\; {\mathbf b}] = \left[\begin{array}{cccc\vert c}
a_{11} & ...
... \vdots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \end{array}\right]$](img431.png)
![$\displaystyle \left[\begin{array}{cccc\vert c}
c_{11} & c_{12} & \cdots & c_{1n...
... \ddots & \vdots & \vdots \\
0 & 0 & \cdots & c_{mn} & d_m \end{array}\right].$](img432.png)
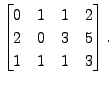 The method proceeds along the
following steps.
The method proceeds along the
following steps.


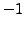 times the
times the



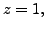 the second equation now gives
the second equation now gives 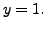 Finally the first equation gives
Finally the first equation gives ![]() Hence the set of
solutions is
Hence the set of
solutions is
![]() A UNIQUE
SOLUTION.
A UNIQUE
SOLUTION.
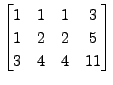 and the method proceeds as follows:
and the method proceeds as follows:



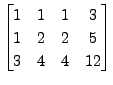 and the method proceeds as follows:
and the method proceeds as follows: