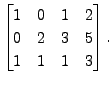Next: Gauss Elimination Method Up: Linear System of Equations Previous: A Solution Method Contents
(compare the system (2.1.2) with the original system.)
(compare the system (2.1.3) with (2.1.2) or the system (2.1.4) with (2.1.3).)
So, in Example 2.1.4, the application of a finite number of elementary operations helped us to obtain a simpler system whose solution can be obtained directly. That is, after applying a finite number of elementary operations, a simpler linear system is obtained which can be easily solved. Note that the three elementary operations defined above, have corresponding INVERSE operations, namely,
It will be a useful exercise for the reader to IDENTIFY THE INVERSE OPERATIONS at each step in Example 2.1.4.
The linear systems at each step in Example 2.1.4 are equivalent to each other and also to the original linear system.
In this case, the systems
![]() and
and
![]() vary only in
the
vary only in
the
![]() equation.
Let
equation.
Let
![]() be a solution of the linear
system
be a solution of the linear
system
![]() Then substituting for
Then substituting for
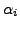 's in place of
's in place of ![]() 's
in the
's
in the
![]() and
and
![]() equations, we get
equations, we get
Therefore,
Use a similar argument to show that if
![]() is a solution of the linear system
is a solution of the linear system
![]() then it is also a
solution of the linear system
then it is also a
solution of the linear system
![]()
Hence, we have the proof in this case. height6pt width 6pt depth 0pt
Lemma 2.2.4 is now used as an induction step to prove the main result of this section (Theorem 2.2.5).
If ![]() Lemma 2.2.4 answers the
question. If
Lemma 2.2.4 answers the
question. If 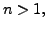 assume that the theorem is true for
assume that the theorem is true for ![]() Now, suppose
Now, suppose 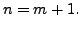 Apply the Lemma 2.2.4 again
at the ``last step" (that is, at the
Apply the Lemma 2.2.4 again
at the ``last step" (that is, at the
![]() step from
the
step from
the
![]() step) to get the required result using
induction.
height6pt width 6pt depth 0pt
step) to get the required result using
induction.
height6pt width 6pt depth 0pt
Let us formalise the above section which led to
Theorem 2.2.5. For solving a linear system of
equations, we applied elementary operations to equations. It is
observed that in performing the elementary operations, the calculations
were made on the COEFFICIENTS (numbers).
The variables
![]() and the sign
of equality (that is,
and the sign
of equality (that is, ![]() )
are not disturbed. Therefore, in place of
looking at the system of equations as a whole, we just need to
work with the coefficients. These coefficients when arranged in a
rectangular array gives us the augmented matrix
)
are not disturbed. Therefore, in place of
looking at the system of equations as a whole, we just need to
work with the coefficients. These coefficients when arranged in a
rectangular array gives us the augmented matrix
![]()
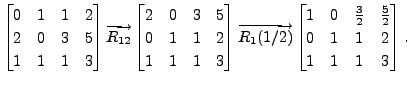
Whereas the matrix
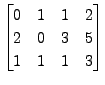 is not row equivalent to the matrix
is not row equivalent to the matrix