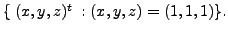EXAMPLE 2.1.4
Let us solve the linear system
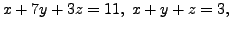 and
and
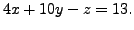
Solution:
- The above linear system and the linear system
have the same set of solutions. (why?)
- Using the
 equation, we eliminate
equation, we eliminate 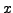 from
from
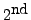 and
and
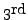 equation to get the linear system
equation to get the linear system
This system and the system (2.1.2)
has the same set of solution. (why?)
- Using the
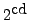 equation, we eliminate
equation, we eliminate 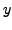 from the
last equation of system (2.1.3) to get the system
from the
last equation of system (2.1.3) to get the system
which has the same set of solution as the system
(2.1.3). (why?)
- The system (2.1.4)
and system
has the same set of solution. (why?)
- Now,
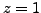 implies
implies
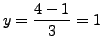 and
and
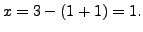 Or in terms of a vector, the set of solution is
Or in terms of a vector, the set of solution is
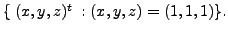
A K Lal
2007-09-12
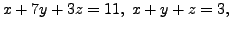 and
and
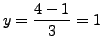 and
and