Let us look at some examples of linear systems.
- Suppose
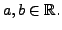 Consider the system
Consider the system 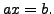
- If
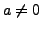 then the system has a
UNIQUE SOLUTION
then the system has a
UNIQUE SOLUTION
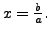
- If
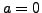 and
and
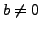 then the system has NO SOLUTION.
then the system has NO SOLUTION.
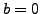 then the system has INFINITE NUMBER OF SOLUTIONS,
namely all
then the system has INFINITE NUMBER OF SOLUTIONS,
namely all
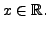
- We now consider a system with
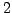 equations in
equations in 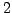 unknowns.
unknowns.
Consider the equation
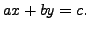 If one of the coefficients,
If one of the coefficients, 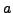 or
or 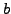 is non-zero, then this linear equation
represents a line in
is non-zero, then this linear equation
represents a line in
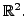 Thus for the system
Thus for the system
the set of solutions is given by the points of
intersection of the two lines. There are three cases to be considered.
Each case is illustrated by an example.
- UNIQUE SOLUTION
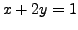 and
and
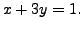 The unique solution is
The unique solution is
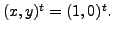
Observe that in this case,
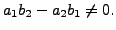
- INFINITE NUMBER OF SOLUTIONS
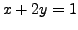 and
and
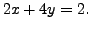 The set of solutions is
The set of solutions is
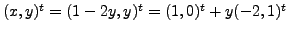 with
with 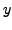 arbitrary. In other words, both the equations
represent the same line.
arbitrary. In other words, both the equations
represent the same line.
Observe that in this case,
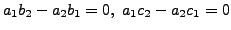 and
and
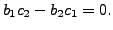
- NO SOLUTION
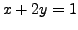 and
and
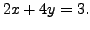 The equations represent a pair of
parallel lines and hence there is no point of intersection.
The equations represent a pair of
parallel lines and hence there is no point of intersection.
Observe that in this case,
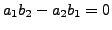 but
but
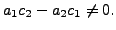
- As a last example, consider
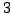 equations in
equations in 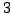 unknowns.
unknowns.
A linear equation
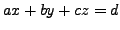 represent a plane in
represent a plane in
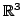 provided
provided
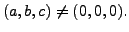 As in the
case of
As in the
case of 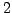 equations in
equations in 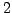 unknowns, we have to look at the
points of intersection of the given three planes. Here again, we
have three cases. The three cases are illustrated by examples.
unknowns, we have to look at the
points of intersection of the given three planes. Here again, we
have three cases. The three cases are illustrated by examples.
- UNIQUE SOLUTION
Consider the system
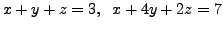 and
and
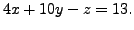 The unique solution to
this system is
The unique solution to
this system is
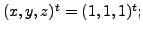 i.e. THE THREE
PLANES INTERSECT AT A POINT.
i.e. THE THREE
PLANES INTERSECT AT A POINT.
- INFINITE NUMBER OF SOLUTIONS
Consider the system
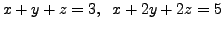 and
and
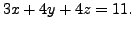 The set of solutions to this system is
The set of solutions to this system is
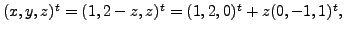 with
with 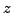 arbitrary: THE THREE PLANES INTERSECT ON A LINE.
arbitrary: THE THREE PLANES INTERSECT ON A LINE.
- NO SOLUTION
The system
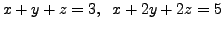 and
and
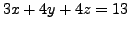 has no solution. In this
case, we get three parallel lines as intersections of the above planes taken
two at a time.
has no solution. In this
case, we get three parallel lines as intersections of the above planes taken
two at a time.
The readers are advised to supply the proof.
We rewrite the above equations in the form
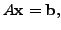 where
where
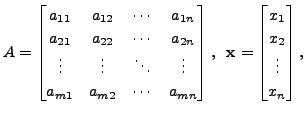 and
and
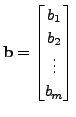
The matrix  is called the
COEFFICIENT matrix and the block matrix
is called the
COEFFICIENT matrix and the block matrix
![$ \left[ A \; \; {\mathbf b}\right],$](img355.png) is the AUGMENTED matrix of the
linear system (2.1.1).
is the AUGMENTED matrix of the
linear system (2.1.1).
Remark 2.1.2
Observe that the
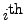 row of the augmented
matrix
row of the augmented
matrix
![$ [A \;\; {\mathbf b}]$](img356.png) represents the
represents the
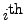 equation and the
equation and the
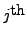 column of the coefficient matrix
column of the coefficient matrix  corresponds to
coefficients of the
corresponds to
coefficients of the
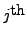 variable
variable 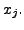 That is,
for
That is,
for
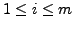 and
and
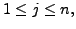 the entry
the entry
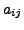 of the coefficient matrix
of the coefficient matrix  corresponds
to the
corresponds
to the
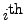 equation and
equation and
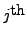 variable
variable 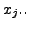
For a system of linear equations
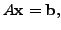 the system
the system
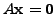 is called the ASSOCIATED HOMOGENEOUS SYSTEM.
is called the ASSOCIATED HOMOGENEOUS SYSTEM.
DEFINITION 2.1.3 (Solution of a Linear System)
A solution of the linear system
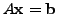 is a column
vector
is a column
vector
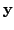 with entries
with entries
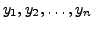 such
that the linear system (2.1.1)
is satisfied by
substituting
such
that the linear system (2.1.1)
is satisfied by
substituting 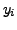 in place of
in place of 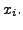
That is, if
![$ {\mathbf y}^t = [ y_1, y_2, \ldots, y_n ]$](img365.png) then
then
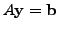 holds.
holds.
Note:
The zero 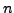 -tuple
-tuple
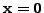 is always a solution of the system
is always a solution of the system
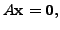 and is called the TRIVIAL solution. A non-zero
and is called the TRIVIAL solution. A non-zero 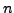 -tuple
-tuple
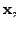 if it satisfies
if it satisfies
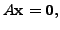 is called a
NON-TRIVIAL solution.
is called a
NON-TRIVIAL solution.
Subsections
A K Lal
2007-09-12
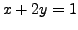 and
and
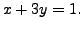 The unique solution is
The unique solution is
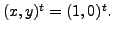
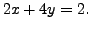 The set of solutions is
The set of solutions is
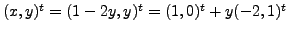 with
with 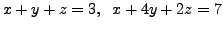 and
and
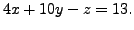 The unique solution to
this system is
The unique solution to
this system is
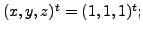 i.e. THE THREE
PLANES INTERSECT AT A POINT.
i.e. THE THREE
PLANES INTERSECT AT A POINT.
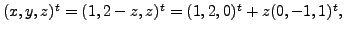 with
with 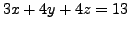 has no solution. In this
case, we get three parallel lines as intersections of the above planes taken
two at a time.
has no solution. In this
case, we get three parallel lines as intersections of the above planes taken
two at a time.
![]() where
where  and
and
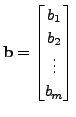
![]() is called the
COEFFICIENT matrix and the block matrix
is called the
COEFFICIENT matrix and the block matrix
![]() is the AUGMENTED matrix of the
linear system (2.1.1).
is the AUGMENTED matrix of the
linear system (2.1.1).
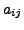 of the coefficient matrix
of the coefficient matrix ![]() the system
the system
![]() is called the ASSOCIATED HOMOGENEOUS SYSTEM.
is called the ASSOCIATED HOMOGENEOUS SYSTEM.
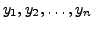 such
that the linear system (2.1.1)
is satisfied by
substituting
such
that the linear system (2.1.1)
is satisfied by
substituting ![]() then
then
![]() holds.
holds.
![]() -tuple
-tuple
![]() is always a solution of the system
is always a solution of the system
![]() and is called the TRIVIAL solution. A non-zero
and is called the TRIVIAL solution. A non-zero ![]() -tuple
-tuple
![]() if it satisfies
if it satisfies
![]() is called a
NON-TRIVIAL solution.
is called a
NON-TRIVIAL solution.