We now start with Step 5
of Example 2.2.11
and apply the elementary operations once again. But this time,
we start with the
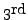 row.
row.
- Add
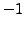 times the third equation to the second equation
(or
times the third equation to the second equation
(or
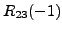 ).
).
- Add
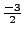 times the third equation to the
first equation (or
times the third equation to the
first equation (or
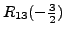 ).
).
- From the above matrix, we directly have the set of solution as
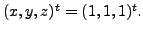
DEFINITION 2.3.6 (Row Reduced Echelon Form of a Matrix)
A matrix 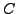 is said to be in the row reduced echelon form if
is said to be in the row reduced echelon form if
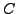 is already in the row reduced form;
is already in the row reduced form;
- The rows consisting of all zeros comes below all non-zero rows; and
- the leading terms appear from left to right in successive rows.
That is, for
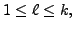 let
let 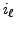 be the leading column of the
be the leading column of the
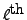 row. Then
row. Then
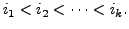
EXAMPLE 2.3.7
Suppose
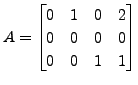 and
and
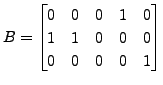 are in row reduced form. Then the
corresponding matrices in the row reduced echelon form are
respectively,
are in row reduced form. Then the
corresponding matrices in the row reduced echelon form are
respectively,
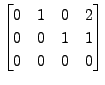 and
and
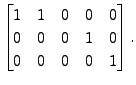
DEFINITION 2.3.8 (Row Reduced Echelon Matrix)
A matrix which is in the row reduced echelon form is also called a
row reduced echelon matrix.
DEFINITION 2.3.9 (Back Substitution/Gauss-Jordan Method)
The procedure to get to Step II of
Example 2.2.11
from Step 5
of Example 2.2.11
is called the back substitution.
The elimination process applied to obtain the row reduced echelon
form of the augmented matrix is called the Gauss-Jordan
elimination.
That is, the Gauss-Jordan elimination method consists of both the
forward elimination and the backward substitution.
Method to get the row-reduced echelon form of a given matrix 
Let  be an
be an
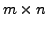 matrix. Then the following method is used
to obtain the row-reduced echelon form the matrix
matrix. Then the following method is used
to obtain the row-reduced echelon form the matrix 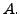
- Step 1: Consider the first column of the matrix
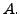
If all the entries in the first
column are zero, move to the second column.
Else, find a row, say
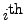 row, which contains a non-zero entry in the first column.
Now, interchange the first row with the
row, which contains a non-zero entry in the first column.
Now, interchange the first row with the
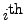 row. Suppose the non-zero entry in the
row. Suppose the non-zero entry in the 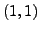 -position
is
-position
is
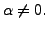 Divide the whole row by
Divide the whole row by 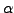 so that the
so that the 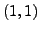 -entry of the new matrix is
-entry of the new matrix is 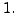 Now, use the
Now, use the 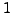 to make all the entries below this
to make all the entries below this 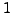 equal to
equal to 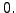
- Step 2: If all entries in the first column after the first step are zero, consider the right
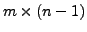 submatrix of the matrix obtained in step 1 and proceed as in step 1.
submatrix of the matrix obtained in step 1 and proceed as in step 1.
Else, forget the first row and first column. Start with the lower
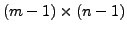 submatrix of the matrix
obtained in the first step and proceed as in step 1.
submatrix of the matrix
obtained in the first step and proceed as in step 1.
- Step 3: Keep repeating this process till we reach a stage where all the entries below a particular row,
say
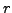 , are zero. Suppose at this stage we have obtained a matrix
, are zero. Suppose at this stage we have obtained a matrix 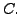 Then
Then 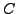 has the following form:
has the following form:
- THE FIRST NON-ZERO ENTRY IN EACH ROW of
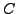 is
is 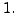 These
These 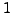 's are the leading terms of
's are the leading terms of 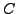 and the
columns containing these leading terms are the leading columns.
and the
columns containing these leading terms are the leading columns.
- THE ENTRIES OF
MATHEND000# BELOW THE LEADING TERM ARE ALL ZERO.
- Step 4: Now use the leading term in the
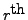 row to make all entries in the
row to make all entries in the
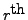 leading column equal to zero.
leading column equal to zero.
- Step 5: Next, use the leading term in the
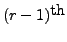 row to make all entries in the
row to make all entries in the
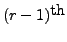 leading column equal to zero and continue till we come to the first leading term or column.
leading column equal to zero and continue till we come to the first leading term or column.
The final matrix is the row-reduced echelon form of the matrix 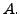
Remark 2.3.10
Note that the row reduction involves only row operations
and proceeds from LEFT TO RIGHT. Hence, if  is a matrix
consisting of first
is a matrix
consisting of first 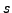 columns of a matrix
columns of a matrix 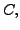 then the
row reduced form of
then the
row reduced form of  will be the first
will be the first 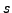 columns of the
row reduced form of
columns of the
row reduced form of 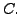
The proof of the following theorem is beyond the scope of this book and
is omitted.
A K Lal
2007-09-12
![]() row.
row.


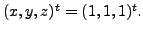
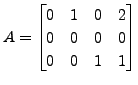 and
and
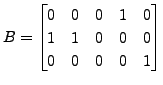 are in row reduced form. Then the
corresponding matrices in the row reduced echelon form are
respectively,
are in row reduced form. Then the
corresponding matrices in the row reduced echelon form are
respectively,
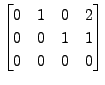 and
and
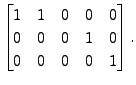
![]()
![]() be an
be an
![]() matrix. Then the following method is used
to obtain the row-reduced echelon form the matrix
matrix. Then the following method is used
to obtain the row-reduced echelon form the matrix ![]()
![]() row, which contains a non-zero entry in the first column.
Now, interchange the first row with the
row, which contains a non-zero entry in the first column.
Now, interchange the first row with the
![]() row. Suppose the non-zero entry in the
row. Suppose the non-zero entry in the ![]() -position
is
-position
is
![]() Divide the whole row by
Divide the whole row by ![]() so that the
so that the ![]() -entry of the new matrix is
-entry of the new matrix is ![]() Now, use the
Now, use the ![]() to make all the entries below this
to make all the entries below this ![]() equal to
equal to ![]()
![]() submatrix of the matrix
obtained in the first step and proceed as in step 1.
submatrix of the matrix
obtained in the first step and proceed as in step 1.
![]()