Dimension of $M + N$

THEOREM 15.4.1   Let $V ({\mathbb{F}})$ be a finite dimensional vector space and let $M$ and $N$ be two subspaces of $V.$ Then

$$\dim (M) + \dim(N) = \dim (M + N) + \dim (M \cap N).$$ (15.4.7)

Proof. Since $M \cap N$ is a vector subspace of $V,$ consider a basis ${\cal B}_1 = \{{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_k \}$ of $M \cap N.$ As, $M \cap N$ is a subspace of the vector spaces $M$ and $N,$ we extend the basis ${\cal B}_1$ to form a basis ${\cal B}_M = \{ {\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_k, {\mathbf v}_1, \ldots, {\mathbf v}_r \}$ of $M$ and also a basis ${\cal B}_N = \{{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_k, {\mathbf w}_1, \ldots, {\mathbf w}_s \}$ of $N.$

We now proceed to prove that that the set ${\cal B}_2 = \{{\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_k, {\mathbf w}_1, \ldots, {\mathbf w}_s, {\mathbf v}_1, {\mathbf v}_2, \ldots, {\mathbf v}_r \}$ is a basis of $M+N.$

To do this, we show that

1. the set ${\cal B}_2$ is linearly independent subset of $V,$ and
2. $L({\cal B}_2) = M + N.$

The second part can be easily verified. To prove the first part, we consider the linear system of equations

$${\alpha}_1 {\mathbf u}_1 + \cdots + {\alpha}_k {\mathbf u}_k + \b... ... w}_s + \gamma_1 {\mathbf v}_1 + \cdots + \gamma_r {\mathbf v}_r = {\mathbf 0}.$$ (15.4.8)

This system can be rewritten as

$${\alpha}_1 {\mathbf u}_1 + \cdots + {\alpha}_k {\mathbf u}_k + \b... ...s {\mathbf w}_s = - (\gamma_1 {\mathbf v}_1 + \cdots + \gamma_r {\mathbf v}_r).$$

The vector ${\mathbf v}= - (\gamma_1 {\mathbf v}_1 + \cdots + \gamma_r {\mathbf v}_r) \in M,$ as ${\mathbf v}_1, \ldots, {\mathbf v}_r \in {\cal B}_M.$ But we also have ${\mathbf v}= {\alpha}_1 {\mathbf u}_1 + \cdots + {\alpha}_k {\mathbf u}_k + \beta_1 {\mathbf w}_1 + \cdots +\beta_s {\mathbf w}_s \in N$ as the vectors ${\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_k, {\mathbf w}_1, \ldots, {\mathbf w}_s \in {\cal B}_N.$ Hence, ${\mathbf v}\in M \cap N$ and therefore, there exists scalars $\delta_1, \ldots, \delta_k$ such that ${\mathbf v}= \delta_1 {\mathbf u}_1 + \delta_2 {\mathbf u}_2 + \cdots + \delta_k {\mathbf u}_k.$

Substituting this representation of ${\mathbf v}$ in Equation (14.4.8), we get

$$({\alpha}_1 - \delta_1){\mathbf u}_1 + \cdots + ({\alpha}_k - \de... ...hbf u}_k + \beta_1 {\mathbf w}_1 + \cdots +\beta_s {\mathbf w}_s = {\mathbf 0}.$$

But then, the vectors 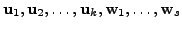${\mathbf u}_1, {\mathbf u}_2, \ldots, {\mathbf u}_k, {\mathbf w}_1, \ldots, {\mathbf w}_s$ are linearly independent as they form a basis. Therefore, by the definition of linear independence, we get

$${\alpha}_i - \delta_i = 0, \; {\mbox{ for }} \; 1 \leq i \leq k \; {\mbox{ and }} \; \beta_j = 0 \; {\mbox{ for }} \; 1 \leq j \leq s.$$

Thus the linear system of Equations (14.4.8) reduces to

$${\alpha}_1 {\mathbf u}_1 + \cdots + {\alpha}_k {\mathbf u}_k + \gamma_1 {\mathbf v}_1 + \cdots + \gamma_r {\mathbf v}_r = {\mathbf 0}.$$

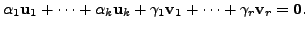
The only solution for this linear system is

$${\alpha}_i = 0, \; {\mbox{ for }} \; 1 \leq i \leq k \; {\mbox{ and }} \; \gamma_j = 0 \; {\mbox{ for }} \; 1 \leq j \leq r.$$

Thus we see that the linear system of Equations (14.4.8) has no non-zero solution. And therefore, the vectors are linearly independent.

Hence, the set ${\cal B}_2$ is a basis of $M+N.$ We now count the vectors in the sets ${\cal B}_1, {\cal B}_2, {\cal B}_M$ and ${\cal B}_N$ to get the required result. height6pt width 6pt depth 0pt