Proof of Rank-Nullity Theorem
THEOREM 15.5.1
Let
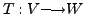 be a linear transformation and
be a linear transformation and
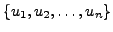 be a basis of
be a basis of  . Then
. Then
-
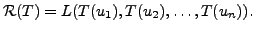
 is one-one
is one-one
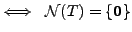 is the zero
subspace of
is the zero
subspace of
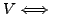
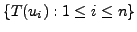 is a basis of
is a basis of
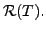
- If
 is finite dimensional vector space then
is finite dimensional vector space then
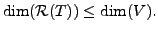 The equality holds if and only if
The equality holds if and only if
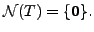
Proof.
Part
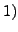
can be easily proved. For
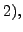
let

be
one-one. Suppose
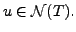
This means that
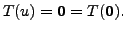
But then

is one-one implies that
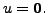
If
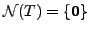
then
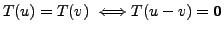
implies that
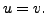
Hence,

is one-one.
The other parts can be similarly proved. Part 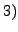 follows from the
previous two parts.
height6pt width 6pt depth 0pt
follows from the
previous two parts.
height6pt width 6pt depth 0pt
The proof of the next theorem is immediate from the fact that
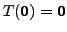 and the definition of linear independence/dependence.
and the definition of linear independence/dependence.
THEOREM 15.5.2
Let
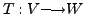 be a linear transformation.
If
be a linear transformation.
If
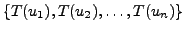 is linearly independent in
is linearly independent in
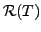 then
then
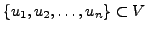 is linearly independent.
is linearly independent.
THEOREM 15.5.3 (Rank Nullity Theorem)
Let
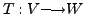 be a linear
transformation and
be a linear
transformation and  be a finite dimensional vector space. Then
be a finite dimensional vector space. Then
or
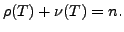
Proof.
Let
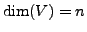
and
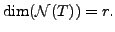
Suppose
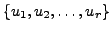
is a basis of
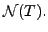
Since
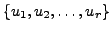
is a linearly independent set in
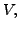
we can
extend it to form a basis of
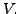
Now there exists vectors
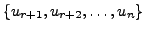
such that the set
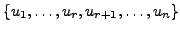
is a basis of
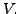
Therefore,
which is equivalent to showing that
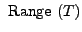
is the span of
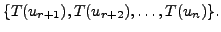
We now prove that the set
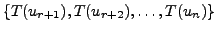 is a linearly independent set. Suppose the set is
linearly dependent. Then, there exists scalars,
is a linearly independent set. Suppose the set is
linearly dependent. Then, there exists scalars,
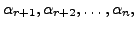 not all zero such that
not all zero such that
Or
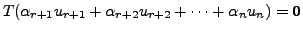
which in turn implies
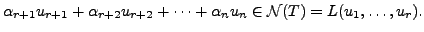
So, there exists scalars
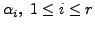
such that
That is,
Thus
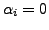
for
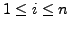
as
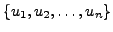
is a basis of
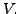
In other words, we have shown that the set
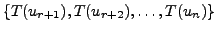
is a basis of
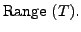
Now, the required result follows.
height6pt width 6pt depth 0pt
we now state another important implication of the Rank-nullity theorem.
COROLLARY 15.5.4
Let
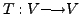 be a linear transformation on a finite dimensional
vector space
be a linear transformation on a finite dimensional
vector space 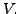 Then
Then
Proof.
Let
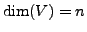
and let

be one-one. Then
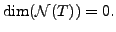
Hence, by the rank-nullity Theorem
14.5.3
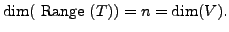
Also,
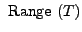
is a subspace of
Hence,
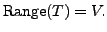
That is,

is onto.
Suppose  is onto. Then
is onto. Then
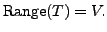 Hence,
Hence,
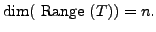 But then by the rank-nullity Theorem
14.5.3,
But then by the rank-nullity Theorem
14.5.3,
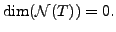 That is,
That is,  is
one-one.
is
one-one.
Now we can assume that  is one-one and onto. Hence, for every vector
is one-one and onto. Hence, for every vector
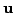 in the range, there is a unique vectors
in the range, there is a unique vectors
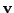 in the domain such that
in the domain such that
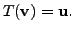 Therefore, for every
Therefore, for every
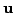 in the range,
we define
in the range,
we define
That is,

has an inverse.
Let us now assume that  has an inverse. Then it is clear that
has an inverse. Then it is clear that  is
one-one and onto.
height6pt width 6pt depth 0pt
is
one-one and onto.
height6pt width 6pt depth 0pt
A K Lal
2007-09-12
![]() follows from the
previous two parts.
height6pt width 6pt depth 0pt
follows from the
previous two parts.
height6pt width 6pt depth 0pt
![]() and the definition of linear independence/dependence.
and the definition of linear independence/dependence.
![]() is a linearly independent set. Suppose the set is
linearly dependent. Then, there exists scalars,
is a linearly independent set. Suppose the set is
linearly dependent. Then, there exists scalars,
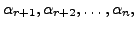 not all zero such that
not all zero such that
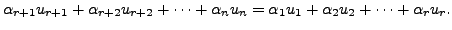
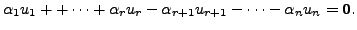
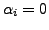 for
for
![]() is onto. Then
is onto. Then
![]() Hence,
Hence,
![]() But then by the rank-nullity Theorem
14.5.3,
But then by the rank-nullity Theorem
14.5.3,
![]() That is,
That is, ![]() is
one-one.
is
one-one.
![]() is one-one and onto. Hence, for every vector
is one-one and onto. Hence, for every vector
![]() in the range, there is a unique vectors
in the range, there is a unique vectors
![]() in the domain such that
in the domain such that
![]() Therefore, for every
Therefore, for every
![]() in the range,
we define
in the range,
we define 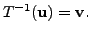
![]() has an inverse. Then it is clear that
has an inverse. Then it is clear that ![]() is
one-one and onto.
height6pt width 6pt depth 0pt
is
one-one and onto.
height6pt width 6pt depth 0pt