Next: About this document ... Up: Appendix Previous: Proof of Rank-Nullity Theorem Contents
Let ![]() be a region in
be a region in 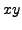 -plane and let
-plane and let ![]() and
and ![]() be real valued
functions defined on
be real valued
functions defined on
![]() Consider an equation
Consider an equation
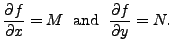
Conversely, let Equation (14.6.10) hold. We now
show that Equation (14.6.10) is exact. Define
![]() on
on ![]() by
by
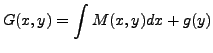
where
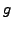 is any arbitrary
smooth function. Then
is any arbitrary
smooth function. Then
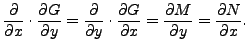
So
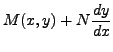 |
![$\displaystyle \frac{\partial G}{\partial x} +
\left[ \frac{\partial G}{\partial y} + \phi(y)\right] \frac{dy}{dx}$](img6014.png) |
||
![$\displaystyle \left[ \frac{\partial G}{\partial x} + \frac{\partial G}{\partial...
...rac{dy}{dx} \right]
+ \frac{d}{dy} \left( \int \phi(y) dy \right) \frac{dy}{dx}$](img6015.png) |
|||
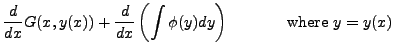 |
|||
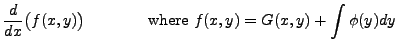 |
A K Lal 2007-09-12