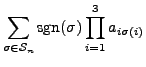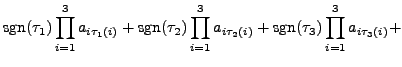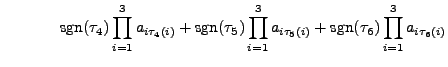In this section, 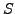 denotes the set
denotes the set
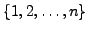 .
.
DEFINITION 15.2.1
- A function
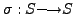 is called a permutation on
is called a permutation on 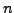 elements if
elements if 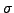 is both one to one and onto.
is both one to one and onto.
- The set of all functions
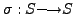 that are both one to one and onto will be denoted
by
that are both one to one and onto will be denoted
by
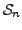 . That is,
. That is,
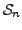 is the set of all permutations of the set
is the set of all permutations of the set
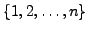 .
.
EXAMPLE 15.2.2
- In general, we represent a permutation
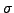 by
by
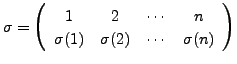 . This representation
of a permutation is called a TWO ROW NOTATION for
. This representation
of a permutation is called a TWO ROW NOTATION for 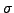 .
.
- For each positive integer
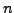 ,
,
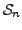 has a special permutation called the identity permutation,
denoted
has a special permutation called the identity permutation,
denoted 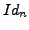 , such that
, such that
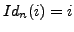 for
for
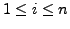 . That is,
. That is,
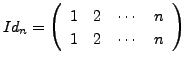 .
.
- Let
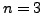 . Then
. Then
Remark 15.2.3
- Let
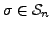 .
Then
.
Then 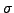 is determined if
is determined if 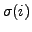 is known for
is known for
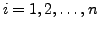 . As
. As 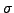 is both one to one
and onto,
is both one to one
and onto,
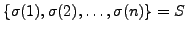 . So, there are
. So, there are 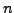 choices for
choices for 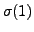 (any
element of
(any
element of 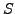 ),
), 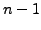 choices for
choices for 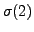 (any element of
(any element of 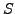 different from
different from 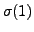 ), and so on.
Hence, there are
), and so on.
Hence, there are
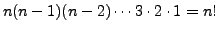 possible permutations. Thus,
the number of elements in
possible permutations. Thus,
the number of elements in
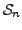 is
is 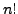 . That is,
. That is,
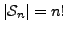 .
.
- Suppose that
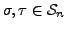 . Then both
. Then both 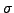 and
and 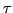 are one to one and onto. So, their
composition map
are one to one and onto. So, their
composition map
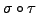 , defined by
, defined by
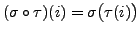 ,
is also both one to one and onto. Hence,
,
is also both one to one and onto. Hence,
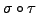 is also a permutation. That is,
is also a permutation. That is,
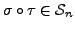 .
.
- Suppose
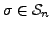 . Then
. Then 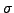 is both one to one and onto. Hence, the function
is both one to one and onto. Hence, the function
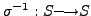 defined by
defined by
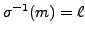 if and only if
if and only if
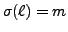 for
for
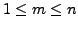 ,
is well defined and indeed
,
is well defined and indeed
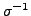 is also both one to one and onto. Hence,
for every element
is also both one to one and onto. Hence,
for every element
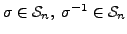 and is the inverse of
and is the inverse of 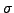 .
.
- Observe that for any
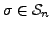 , the compositions
, the compositions
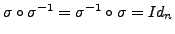 .
.
Proof.
For the first part, we need to show that given any element
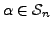
, there exists elements
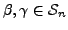
such that
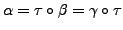
.
It can easily be verified that
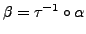
and
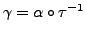
.
For the second part, note that for any
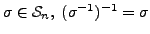 . Hence the result holds.
height6pt width 6pt depth 0pt
. Hence the result holds.
height6pt width 6pt depth 0pt
DEFINITION 15.2.5
Let
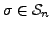 . Then the number of inversions of
. Then the number of inversions of 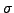 , denoted
, denoted 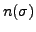 , equals
, equals
Note that, for any
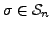 ,
, 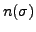 also equals
also equals
DEFINITION 15.2.6
A permutation
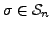 is called a transposition if there exists two positive integers
is called a transposition if there exists two positive integers
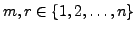 such that
such that
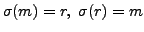 and
and
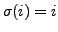 for
for
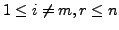 .
.
For the sake of convenience, a transposition 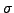 for which
for which
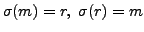 and
and
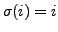 for
for
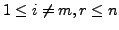 will be denoted simply by
will be denoted simply by
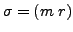 or
or 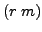 . Also, note that for any transposition
. Also, note that for any transposition
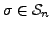 ,
,
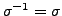 . That is,
. That is,
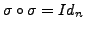 .
.
With the above definitions, we state and prove two important results.
THEOREM 15.2.8
For any
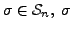 can be written as composition (product) of transpositions.
can be written as composition (product) of transpositions.
Proof.
We will prove the result by induction on
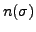
, the number of inversions
of
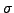
. If
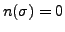
, then
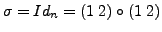
.
So, let the result be true for all
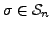
with
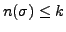
.
For the next step of the induction, suppose that
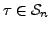 with
with
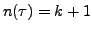 . Choose the smallest
positive number, say
. Choose the smallest
positive number, say 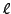 , such that
, such that
As
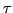
is a permutation, there exists a positive number, say
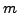
,
such that
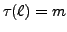
. Also, note that
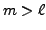
. Define a transposition
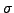
by
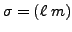
. Then note that
So, the definition
of ``number of inversions" and
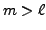
implies that
Thus,
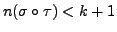
. Hence, by the induction hypothesis, the permutation
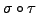
is a composition of transpositions. That is, there exist transpositions,
say
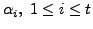
such that
Hence,
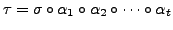
as
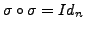
for any transposition
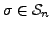
.
Therefore, by mathematical induction, the proof of the theorem is complete.
height6pt width 6pt depth 0pt
Before coming to our next important result, we state and prove the following lemma.
LEMMA 15.2.9
Suppose there exist transpositions
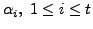 such that
such that
then 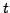 is even.
is even.
Proof.
Observe that
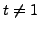
as the identity permutation is not a transposition. Hence,
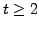
.
If
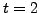
, we are done. So, let us assume that
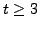
. We will prove the result by the method of
mathematical induction. The result clearly holds for
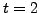
. Let the result be true for all
expressions in which the number of transpositions
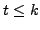
. Now, let
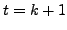
.
Suppose
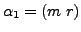 . Note that the possible choices for the composition
. Note that the possible choices for the composition
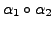 are
are
where
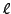
and
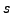
are distinct elements of
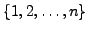
and are different from
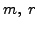
.
In the first case, we can remove
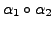
and obtain
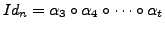
.
In this expression for identity, the number of transpositions is
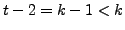
. So, by mathematical induction,
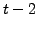
is even and hence
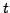
is also even.
In the other three cases, we replace the original expression for
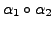 by their counterparts
on the right to obtain another expression for identity in terms of
by their counterparts
on the right to obtain another expression for identity in terms of 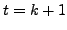 transpositions. But note that in
the new expression for identity, the positive integer
transpositions. But note that in
the new expression for identity, the positive integer 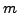 doesn't appear in the first transposition,
but appears in the second transposition. We can continue the above process with the second and third transpositions.
At this step, either the number of transpositions will reduce by
doesn't appear in the first transposition,
but appears in the second transposition. We can continue the above process with the second and third transpositions.
At this step, either the number of transpositions will reduce by 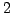 (giving us the result by mathematical
induction) or the positive number
(giving us the result by mathematical
induction) or the positive number 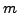 will get shifted to the third transposition. The continuation of this process
will at some stage lead to an expression for identity in which the number of transpositions is
will get shifted to the third transposition. The continuation of this process
will at some stage lead to an expression for identity in which the number of transpositions is 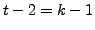 (which will give us the desired result by mathematical induction), or else we will have
an expression in which the positive number
(which will give us the desired result by mathematical induction), or else we will have
an expression in which the positive number 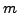 will get shifted to
the right most transposition. In the later case, the positive integer
will get shifted to
the right most transposition. In the later case, the positive integer 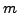 appears exactly once in the expression
for identity and hence this expression does not fix
appears exactly once in the expression
for identity and hence this expression does not fix 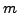 whereas for the identity permutation
whereas for the identity permutation
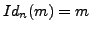 .
So the later case leads us to a contradiction.
.
So the later case leads us to a contradiction.
Hence, the process will surely lead to an expression in which the
number of transpositions at some stage is 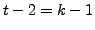 . Therefore, by mathematical induction,
the proof of the lemma is complete.
. Therefore, by mathematical induction,
the proof of the lemma is complete.
height6pt width 6pt depth 0pt
Proof.
Observe that the condition
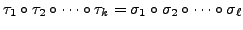
and
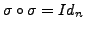
for any transposition
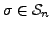
, implies that
Hence by Lemma
14.2.9,
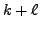
is even. Hence, either
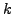
and
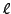
are both even or
both odd. Thus the result follows.
height6pt width 6pt depth 0pt
DEFINITION 15.2.11
A permutation
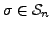 is called an even permutation if
is called an even permutation if 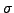 can be written as a composition
(product) of an even number of transpositions. A permutation
can be written as a composition
(product) of an even number of transpositions. A permutation
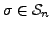 is called an odd permutation if
is called an odd permutation if 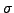 can be written as a composition (product) of an odd number of transpositions.
can be written as a composition (product) of an odd number of transpositions.
Remark 15.2.12
Observe that if 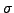 and
and 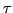 are both even or both odd permutations, then the permutations
are both even or both odd permutations, then the permutations
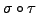 and
and
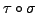 are both even. Whereas if one of them is odd and the other even then the
permutations
are both even. Whereas if one of them is odd and the other even then the
permutations
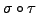 and
and
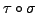 are both odd. We use this to define a function
on
are both odd. We use this to define a function
on
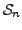 , called the sign of a permutation, as follows:
, called the sign of a permutation, as follows:
DEFINITION 15.2.13
Let
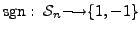 be a function defined by
be a function defined by
EXAMPLE 15.2.14
- The identity permutation,
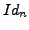 is an even permutation whereas every transposition is an odd permutation.
Thus,
is an even permutation whereas every transposition is an odd permutation.
Thus,
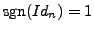 and for any transposition
and for any transposition
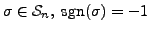 .
.
- Using Remark 14.2.12,
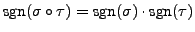 for any two permutations
for any two permutations
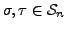 .
.
We are now ready to define determinant of a square matrix 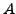 .
.
Remark 15.2.16
- Observe that
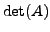 is a scalar quantity. The expression for
is a scalar quantity. The expression for 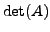 seems complicated at the first
glance. But this expression is very helpful in proving the results related with ``properties of determinant".
seems complicated at the first
glance. But this expression is very helpful in proving the results related with ``properties of determinant".
- If
![$ A=[a_{ij}]$](img20.png) is a
is a
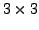 matrix, then using (14.2.5),
matrix, then using (14.2.5),
Observe that this expression for 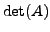 for a
for a
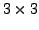 matrix
matrix 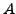 is same as that given in (2.6.1).
is same as that given in (2.6.1).
A K Lal
2007-09-12
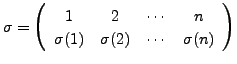 . This representation
of a permutation is called a TWO ROW NOTATION for
. This representation
of a permutation is called a TWO ROW NOTATION for 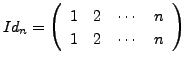 .
.
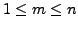 ,
is well defined and indeed
,
is well defined and indeed
![]() . Hence the result holds.
height6pt width 6pt depth 0pt
. Hence the result holds.
height6pt width 6pt depth 0pt
![]() ,
, ![]() also equals
also equals 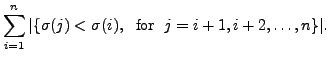
![]() for which
for which
![]() and
and
![]() for
for
![]() will be denoted simply by
will be denoted simply by
![]() or
or ![]() . Also, note that for any transposition
. Also, note that for any transposition
![]() ,
,
![]() . That is,
. That is,
![]() .
.
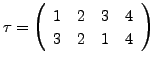 is a transposition as
is a transposition as
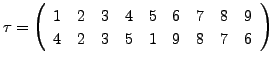 . Then check that
. Then check that 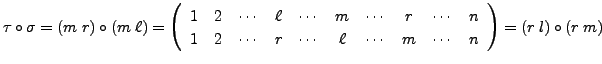 . Similarly check that
. Similarly check that
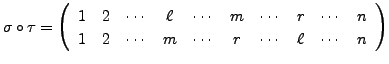 .
.
![]() with
with
![]() . Choose the smallest
positive number, say
. Choose the smallest
positive number, say ![]() , such that
, such that 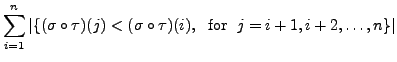
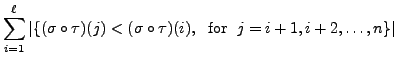
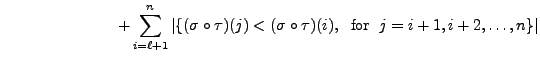
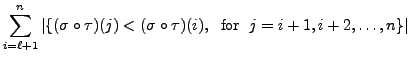
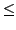
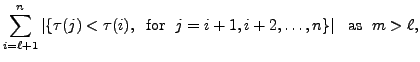
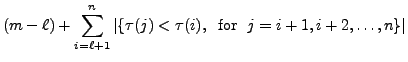
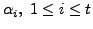 such that
such that
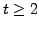 .
If
.
If ![]() . Note that the possible choices for the composition
. Note that the possible choices for the composition
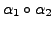 are
are
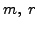 .
In the first case, we can remove
.
In the first case, we can remove
![]() by their counterparts
on the right to obtain another expression for identity in terms of
by their counterparts
on the right to obtain another expression for identity in terms of ![]() transpositions. But note that in
the new expression for identity, the positive integer
transpositions. But note that in
the new expression for identity, the positive integer ![]() doesn't appear in the first transposition,
but appears in the second transposition. We can continue the above process with the second and third transpositions.
At this step, either the number of transpositions will reduce by
doesn't appear in the first transposition,
but appears in the second transposition. We can continue the above process with the second and third transpositions.
At this step, either the number of transpositions will reduce by ![]() (giving us the result by mathematical
induction) or the positive number
(giving us the result by mathematical
induction) or the positive number ![]() will get shifted to the third transposition. The continuation of this process
will at some stage lead to an expression for identity in which the number of transpositions is
will get shifted to the third transposition. The continuation of this process
will at some stage lead to an expression for identity in which the number of transpositions is ![]() (which will give us the desired result by mathematical induction), or else we will have
an expression in which the positive number
(which will give us the desired result by mathematical induction), or else we will have
an expression in which the positive number ![]() will get shifted to
the right most transposition. In the later case, the positive integer
will get shifted to
the right most transposition. In the later case, the positive integer ![]() appears exactly once in the expression
for identity and hence this expression does not fix
appears exactly once in the expression
for identity and hence this expression does not fix ![]() whereas for the identity permutation
whereas for the identity permutation
![]() .
So the later case leads us to a contradiction.
.
So the later case leads us to a contradiction.
![]() . Therefore, by mathematical induction,
the proof of the lemma is complete.
. Therefore, by mathematical induction,
the proof of the lemma is complete.
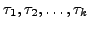 and
and
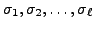 such that
such that
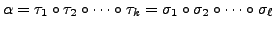
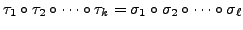 and
and
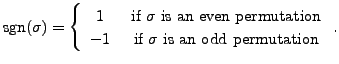
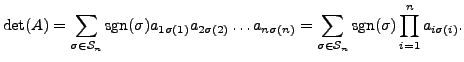
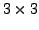 matrix, then using (14.2.5),
matrix, then using (14.2.5),