Next: Linear Transformations Up: Finite Dimensional Vector Spaces Previous: Important Results Contents
Let
![]() be a basis of a vector space
be a basis of a vector space
![]() As
As ![]() is a set, there is no ordering of its elements.
In this section, we want to associate an order among the vectors
in any basis of
is a set, there is no ordering of its elements.
In this section, we want to associate an order among the vectors
in any basis of ![]()
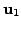 as the first vector,
as the first vector,
For any element
![]() we have
we have
If
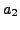 is the third
component of the vector
is the third
component of the vector
If we take
![]() as an ordered basis, then
as an ordered basis, then
![]() is the first component,
is the first component,
![]() is the second component, and
is the second component, and ![]() is the third
component of the vector
is the third
component of the vector
![]()
That is, as ordered bases
![]()
![]() and
and
![]() are different even though they have the
same set of vectors as elements.
are different even though they have the
same set of vectors as elements.
then the tuple
Mathematically, we denote it by
![$ [{\mathbf v}]_{{\cal B}} = (\beta_1, \ldots, \beta_n)^t,$](img1585.png) A COLUMN VECTOR.
A COLUMN VECTOR.
Suppose
![]() and
and
![]() are two ordered bases of
are two ordered bases of ![]() Then for any
Then for any
![]() there exists unique scalars
there exists unique scalars
![]() such that
such that
Therefore,
![$\displaystyle [{\mathbf x}]_{{\cal B}_1} = ({\alpha}_1, {\alpha}_2, \ldots, {\a...
...thbf x}]_{{\cal B}_2} = (\alpha_n, \alpha_1, \alpha_2,
\ldots, \alpha_{n-1})^t.$](img1591.png)
Note that
![]() is uniquely
written as
is uniquely
written as
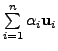 and hence the
coordinates with respect to an ordered basis are unique.
and hence the
coordinates with respect to an ordered basis are unique.
Suppose that the ordered basis
![]() is changed to the
ordered basis
is changed to the
ordered basis
![]() Then
Then
![$ [{\mathbf x}]_{{\cal B}_3} = (\alpha_2, \alpha_1,
\alpha_3, \ldots, \alpha_n )^t.$](img1595.png) So, the coordinates of a
vector depend on the ordered basis chosen.
So, the coordinates of a
vector depend on the ordered basis chosen.
In general, let ![]() be an
be an ![]() -dimensional vector space with
ordered bases
-dimensional vector space with
ordered bases
![]() and
and
![]() Since,
Since,
![]() is a basis of
is a basis of ![]() there exists unique scalars
there exists unique scalars
![]() such
that
such
that
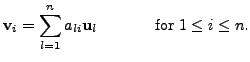
That is, for each
![$ i, \; 1 \leq i \leq n, \; [{\mathbf v}_i]_{{\cal B}_1} =
(a_{1i}, a_{2i}, \ldots, a_{ni})^t.$](img1609.png)
Let
![]() with
with
![$ [{\mathbf v}]_{{\cal B}_2}
= (\alpha_1, \alpha_2, \ldots, \alpha_n)^t.$](img1610.png) As
As
![]() as
ordered basis
as
ordered basis
![]() we have
we have
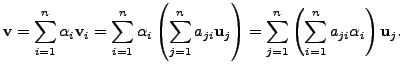
Since
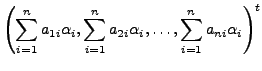 |
|||
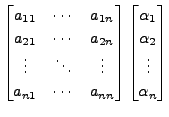 |
|||
![$ A = [a_{ij}] = \begin{bmatrix}0 & 2 & 0\\ 0 &
-2 & 1 \\ 1 & 1 & 0 \end{bmatrix}.$](img1633.png) The columns of the matrix
The columns of the matrix
and
That is, the elements of
![$\displaystyle [(x,y,z)]_{{\cal B}_1} = \begin{bmatrix}x-y\\ y-z\\ z \end{bmatri...
...-x}{2} + z\\ \frac{x-y}{2}\\ x-z \end{bmatrix} =A \; \; [(x,y,z)]_{{\cal B}_2}.$](img1638.png)
In the next chapter, we try to understand Theorem 3.4.5 again using the ideas of `linear transformations / functions'.
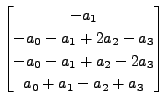 |
|||
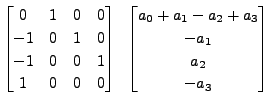 |
|||