Next: Examples Up: Vector Spaces Previous: Vector Spaces Contents
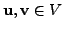 there corresponds a unique
element
there corresponds a unique
element
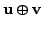 in
in 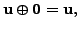 for every
for every
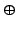 is called VECTOR ADDITION.
is called VECTOR ADDITION.
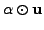 in
in 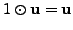 for every
for every
Note: the number 0
is the element of
![]() whereas
whereas
![]() is the
zero vector.
is the
zero vector.
We may sometimes write ![]() for a vector space if
for a vector space if
![]() is understood from the
context.
is understood from the
context.
Some interesting consequences of Definition 3.1.1 is the following useful result. Intuitively, these results seem to be obvious but for better understanding of the axioms it is desirable to go through the proof.
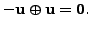
Hence,
![]() is equivalent to
is equivalent to
Proof of Part 2.
As
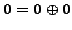 , using the distributive law, we have
, using the distributive law, we have
Thus, for any
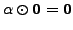 .
In the same way,
.
In the same way,
Hence, using the first part, one has
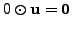 for any
for any
Now suppose
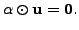 If
If
![]() then
the proof is over. Therefore, let us assume
then
the proof is over. Therefore, let us assume
![]() (note that
(note that
![]() is a real or complex number, hence
is a real or complex number, hence
![]() exists and
exists and
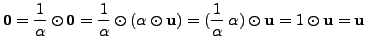
as
Thus we have shown that if
![]() and
and
![]() then
then
![]()
Proof of Part 3.
We have
![]() and
hence
and
hence
![]() height6pt width 6pt depth 0pt
height6pt width 6pt depth 0pt
A K Lal 2007-09-12