| |
Extending to three dimensions, the electric field is given by |
| |
where 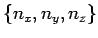 is a set of positive integers. (If any of these inegers is zero, it gives zero field. Taking negative values of the integers do not give different fields as it amounts to simply multiplying is a set of positive integers. (If any of these inegers is zero, it gives zero field. Taking negative values of the integers do not give different fields as it amounts to simply multiplying 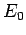 by a sign factor.) Substituting Eqn. (1) in the electromagnetic wave equation by a sign factor.) Substituting Eqn. (1) in the electromagnetic wave equation |