 |
where the constant of proportionality 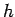 is called Planck's constant . Its value in SI units is is called Planck's constant . Its value in SI units is 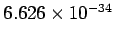 J-s. Thus the possible energy of a mode with frequency J-s. Thus the possible energy of a mode with frequency 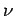 is is 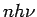 where where 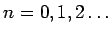 . According to Boltzmann distribution, the probability of a mode having an energy . According to Boltzmann distribution, the probability of a mode having an energy 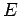 at a temperature at a temperature 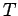 is given by is given by 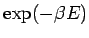 , where , where 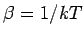 . Here, . Here, 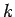 is the Boltzmann constant and is the Boltzmann constant and 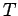 is the absolute temperature. Thus the average energy of a mode is is the absolute temperature. Thus the average energy of a mode is |