| |
Find the temperature for which the radiant energy density at a wavelength of 200 nm is four times that of the density at 400 nm. |
| |
Substituting values of 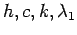 and and 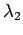 , we get , we get |
| |
which gives, on simplification 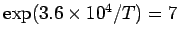 . On solving, the temperature works out approximately to be 18,500 K. . On solving, the temperature works out approximately to be 18,500 K. |