|
Stefan's Law : The intensity of emitted radiation for a given wavelength is proportional to the fourth power |
| |
of the temperature of the black body. |
|
Wien's law : For a given temperature, the spectrum of emitted radiation has maximum intensity for a |
 |
wavelength 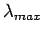 , which is inversely proportional to the temperature of the black body. Thus relatively colder bodies appear red as their maximum intensity is in the red end of the spectrum while hotter bodies appear bluish. Because of this, when we heat a metal wire it firs becomes red hot and then as the temperature increases it become "white hot". , which is inversely proportional to the temperature of the black body. Thus relatively colder bodies appear red as their maximum intensity is in the red end of the spectrum while hotter bodies appear bluish. Because of this, when we heat a metal wire it firs becomes red hot and then as the temperature increases it become "white hot". |
| |
In classical physics, radiation is considered as waves and the calculation of radiant energy emitted by a black body is carried out in the following steps. |
(1) |
We consider the black body to be in the shape of a cubical metal cavity of side 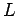 with a small hole in it. with a small hole in it. |
| |
Any radiation which falls on the hole is lost inside the cavity. The radiation which emerges from the hole has the characteristics of the radiation that is trapped inside the cavity. |
(2) |
The waves inside the cavity form standing wave pattern with nodes at the walls of the cavity since the electric |
| |
field must vanish inside a metal. |
| |
If we consider standing waves in one dimension, the electric field having nodes at 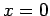 and and 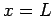 is given by is given by 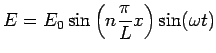 where where 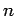 is a positive integer. The pattern of the standing wave is shown. The frequency is a positive integer. The pattern of the standing wave is shown. The frequency 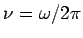 is given by is given by 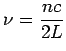 |