(3) |
As the average energy of a mode is 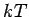 , the radiant energy density, which is defined as the average energy , the radiant energy density, which is defined as the average energy |
| |
per unit volume is given by |
| |
This is known as Rayleigh - Jeans' Law |
(4) |
The radiant intensity can be obtained from the expression for the energy density by multiplying the above |
| |
expression by 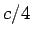 . The curious factor of 1/4 arises because . The curious factor of 1/4 arises because |
|
At any instant, on an average, half of the waves are directed towards the wall of the cavity and another half |
| |
is directed away from it. This gives a factor of 1/2. |
|
We need to average over all angles. In computing the radiant power, we get a factor of 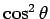 , which averages , which averages |
| |
to 1/2. The radiant intensity is given by |