| |
The frequency 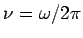 is given by is given by |
 |
For a given frequency, the equation above represents a sphere of radius 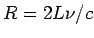 in the three dimensional space of in the three dimensional space of 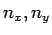 and and 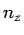 and each value of and each value of 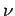 represents a distinct point in this space. Since represents a distinct point in this space. Since 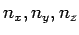 can only take integral values, the number of points per unit volume is one. If we treat can only take integral values, the number of points per unit volume is one. If we treat 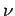 as a continuous variable, the number of modes for frequency less than some given as a continuous variable, the number of modes for frequency less than some given 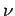 is given by is given by |
| |
where 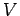 is the volume of the cavity. In the above, the factor of 1/8 comes because we are restricted to the positive octant as is the volume of the cavity. In the above, the factor of 1/8 comes because we are restricted to the positive octant as 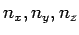 can only be positive. The factor of 2 takes into account the fact that there are two transverse modes. The number of modes in the frequency interval can only be positive. The factor of 2 takes into account the fact that there are two transverse modes. The number of modes in the frequency interval 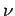 and and 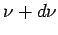 is is |