• The above estimates are simplified and partly empirical, i.e., they do not take directly into account, for example, the effect of the diffusion depth 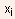on the short channel effects, which may be important.
• Experimental studies show that a transition from long to short channel behavior takes place when
  
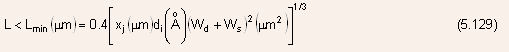
  where are the drain-substrate and source-substrate depletion widths respectively.
  
  
• This expression indicates the importance of the contact depth, however, indirectly, this behavior may also by accounted for by a judicious choice of the adjustable parameter

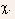
Model for Mobility

• The mobility model, which has gained wide acceptance and is used almost universally (including BSIM) is given by

  

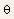  where is referred to as the low-field mobility, and is referred to as the field-degradation coefficient for mobility.
  

• This is an extremely hot area of research, and lots of work in this area is going on around the world.
  

• There are plenty of other models also available in the literature; however, most of these are empirical and based on heuristics.

Hot Electron Effects

• As the device sizes are scaled down, the electric field in the channel increases, and, in the saturation region, the high field region near the drain occupies a large fraction of the channel length.
  

• This leads to the so-called hot electron effects, which manifest themselves in a superlinear increase in the drain current in the saturation region (the kink effect) and in the degradation of device parameters with time.
  

• These effects represent a major obstacle to further scaling down of MOSFET feature sizes.
  
  
• The physics of the hot electron effects can be described as follows.
  
  
• Electrons, while traveling from source to drain through the channel, experience a high field near the drain, and acquire large energy.
  
  
• When the energy thus acquired by an electron becomes equal to or greater than the band gap energy, then these electrons can collide with an atom and create EHPs (impact ionization EHP generation).
  
  
• The generated holes are pushed into the bulk due to the electric field, thus constituting the substrate current, and the electrons increase the drain current in the saturation region, thus causing the kink in the drain current characteristics.
  
  
• Some of these electrons may even acquire such a large energy from this field that they can surmount the barrier and get trapped in the oxide => this gives rise to instability in the device behavior, since these electrons can alter the charge states in the oxide.
  
  
• The process of EHP generation can be described by a generation rate G, which is an exponential function of the maximum electric field in the channel 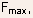, which is reached at the drain:

  
  
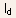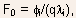  where A is a constant, is the drain current, and is the characteristic field for the impact ionization, given by where 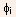is the energy required for an ionization event, and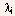 is the mean free path for the ionization process.

• Typical value of 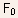is 1.7 mV/cm for Si n-channel MOSFETs.
• The generation rate is proportional to the drain current since it ought to be proportional to the product of the electron sheet density in the channel and the electron velocity.
  

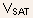• The maximum electric field is given by is the intrinsic drain-source voltage, is the intrinsic drain-source saturation voltage, and 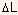is the length of the pinch-off region, given by

  

  where 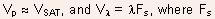is the field required for velocity saturation, and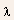 is a characteristic length of the electric field variation in the high field region near the drain and is given by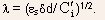
  

• The substrate current 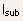is proportional to the generation rate, hence,

  

  where B is a constant
  

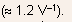
• Equation (5.133) can be rewritten as 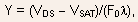where

  

• Analysis shows that only one iteration is sufficient to accurately solve this equation by iteration if 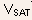is substituted by 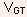in Eq.(5.134).
  Note: the measured values of Y depend linearly on the drain-source voltage in the kink region, thus, Eq.(5.134) can be used for the extraction of the saturation voltage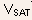 from the experimental data.
  
  
• Hot electrons can also tunnel into traps in the gate oxide near the drain.
  
• The negative charge in the oxide causes partial channel depletion near the drain, leading to an increase in the channel resistance and a decrease in the threshold voltage in this region.
  
• Hence, the device characteristics change with time when the drain voltage is high enough to cause significant electron heating (i.e., under voltage stress).
  
• The increase in the channel resistance should lead to a shift in the drain-source saturation voltage (it increases) and a reduction in the drain-source current.

  

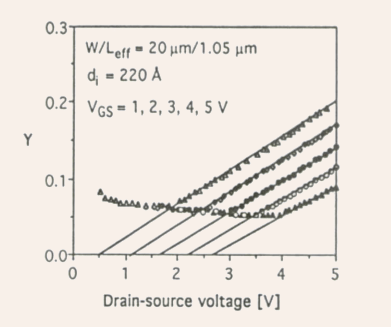
  Fig.5.33 Measured Y versus curves.

  
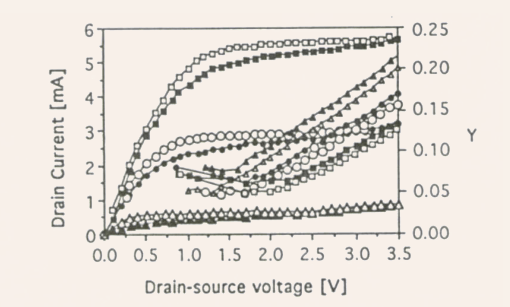
  Fig.5.34

• Measured I-V characteristics and Y-functions for an n-channel Si MOSFET: open symbols data before stress, dark symbols data after stress at 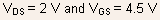for 104 sec.

• As can be seen from Fig.5.34, the Y versus 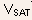curves experience a parallel shift as a result of the voltage stress.
  

• This electron trapping also causes a change 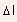in the drain current, given by

  

  where 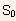is a constant.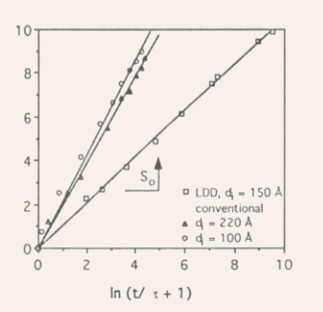

  

• Fig.74 Measured values of 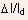(in percent) under stress versus time.
  

MOSFET Models and SPICE Parameters

• A large number of MOSFET models exist in literature, the most popular among them is the BSIM (Berkeley Short-Channel IGFET Model).
  

• Currently, significant research is going on in the area of MOSFET modeling, in order to make these models more accurate in describing device behavior for ultra-short channel length devices.
  
  There are different levels of these models, e.g.
  
  LEVEL 1: Shichman-Hodges
  LEVEL 2: Geometric based analytical model
  LEVEL 3: Semi-empirical short channel model
  LEVEL 4: BSIM
  LEVEL 5: New BSIM (BSIM2)
  LEVEL 6: MOS6 (Sakurai and Newton)
  LEVEL 7: Universal extrinsic short channel model
  LEVEL 8: Unified long channel model (UCCM)
  LEVEL 9: Short channel model
  LEVEL 10: Unified intrinsic short channel model
  LEVEL 11: Unified extrinsic a-Si TFT model
  LEVEL 12: Polysilicon TFT model
  
  The list given above is by no means complete, and there are plenty more new models, which describe short channel device behavior more accurately than their predecessors.
  
  

• For SPICE simulation, the MOS element is defined in the following way:
  

• MX ND NG NS NB MNAME <L=VALUE> <W=VALUE> <AD=VALUE> <AS=VALUE> <PD=VALUE> <PS=VALUE> <NRD=VALUE> <NRS=VALUE> <NRG=VALUE> <NRB = VALUE> <OFF> <IC=VDS,VGS,VBS> <TEMP=T>
  where
  

• MX is the device number;
  

• ND, NG, NS, and NB are the node numbers for the drain, gate, source, and substrate respectively;
  

• L and W are the channel length and channel width respectively,
  

• AD and AS are the areas of the drain and source respectively,
  

• PD and PS are the perimeters of the drain and source respectively,
  

• NRD, NRS, NRG, and NRB are the relative resistivities of the drain, source, gate, and substrate respectively in number of squares,
  

• OFF indicates an optional initial value for the element in a DC analysis,
  

• the optional initial value IC=VDS,VGS,VBS is to be used together with UIC (use initial condition) in a Transient analysis, and the optional TEMP value is the temperature at which this device operates.
  
  Parameters for LEVELs 1, 2, 3, and 6: