
- The series source resistance reduces the drain current, and the
series drain resistance increases the drain-to-source saturation voltage.
- Both series source resistance and series drain resistance reduce the drain conductance at low drain-to-source voltages.
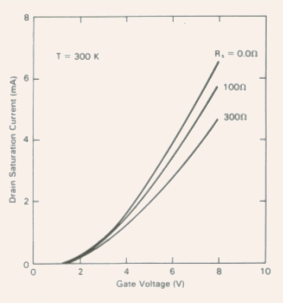
Fig.5.10 The variation of the drain saturation current as a function
of the gate voltage for three different values of the series source
resistance ![]()
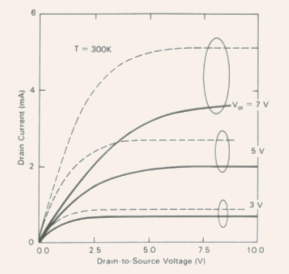
Fig.5.11 The drain current drain-to-source voltage characteristics
for different values of ![]()
![]() Velocity Saturation Effects in MOSFETs
Velocity Saturation Effects in MOSFETs
- In modern day MOSFETs, the channel length is very small, the electric
field in the channel is very high, and the velocity saturation effects
are very important.
- The measured electron and hole mobilities in the inversion layer
may be quite different than those measured in the bulk.
- Note: the channel, in reality, is under a two-dimensional electric
field, one directed longitudinally
 from
the gate to the substrate, and the other directed laterally
from
the gate to the substrate, and the other directed laterally  along
the length of the channel.
along
the length of the channel.
- The effective inversion layer thickness
 is
approximately given by
is
approximately given by  thus,
a large vertical field creates a narrow inversion layer, and vice
versa.
thus,
a large vertical field creates a narrow inversion layer, and vice
versa.
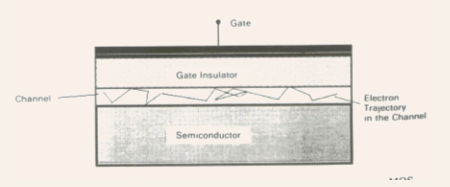
Fig.5.12 The random path of electrons in the channel, undergoing surface scattering, which is more intense in narrow channels. - Electrons in the channel move in random directions, undergoing
surface scattering, which increases for narrow channels
 thus
their mobility drops.
thus
their mobility drops.
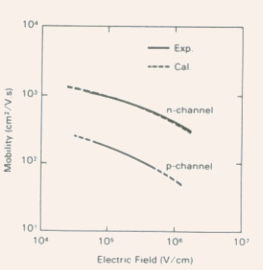
Fig.5.13 The variation of the electron and hole mobilities in the channel as a function of the gate electric field.
- The dependence of the electron and hole mobilities on the gate
field
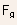 can
be crudely approximated by
can
be crudely approximated by
where n0 and p0 are the electron and hole mobilities for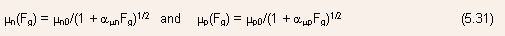
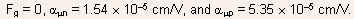
- It is very interesting to note that in highly constricted channels
or at low temperatures, the carrier mobility is seen to get enhanced.
- This is because for these cases, the electron motion in the direction
perpendicular to the
 interface
gets quantized, and the channel electrons behave like a two-dimensional
electron gas (2DEG).
interface
gets quantized, and the channel electrons behave like a two-dimensional
electron gas (2DEG).
- Thus, the surface scattering is not that important, and the impurity
scattering is screened by a high density of electrons in the channel.
- Such enhancement of electron mobility was observed in GaAs, and is exploited in high electron mobility transistors (HEMTs) or modulation-doped field effect transistors (MODFETs).
![]() Effects of Velocity Saturation on the I-V Characteristic
Effects of Velocity Saturation on the I-V Characteristic
- For this derivation, a simple two-piece linear approximation for
the electron velocity is used:
where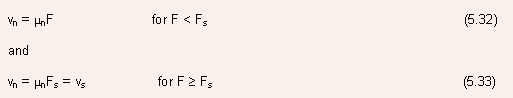
 is
the electric field required for velocity saturation, and
is
the electric field required for velocity saturation, and 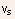 is
the saturation limited thermal velocity.
is
the saturation limited thermal velocity.
- Recall: in the linear region, the I-V characteristic can be given
by:
where
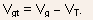
- The saturation current
 can
now be found by assuming that the current saturation occurs when the
electric field at the drain side of the channel exceeds the critical
field
can
now be found by assuming that the current saturation occurs when the
electric field at the drain side of the channel exceeds the critical
field 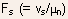 required
for velocity saturation.
required
for velocity saturation.
- This is a much more realistic assumption than the Shockley model,
which assumes saturation occurs when

- The constant mobility model is still used for drain voltages below
the saturation voltage.
- The absolute value of the electric field in the channel
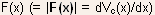 at
drain voltages below the saturation voltage can be obtained from Eq.(5.21):
at
drain voltages below the saturation voltage can be obtained from Eq.(5.21):

- Integrating Eq.(5.35) from 0 to x, the following equation for the
channel potential
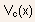 is
obtained for drain voltages below the saturation voltage:
is
obtained for drain voltages below the saturation voltage:

-
The solution of this equation is given by

- Substituting Eq.(5.37) into Eq.(5.35), the following expression
for the electric field as a function of distance is obtained:

and the electric field F(L) at the drain side of the channel (where it is the largest),

-
From the condition
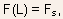 the
drain saturation current can now be found as
the
drain saturation current can now be found as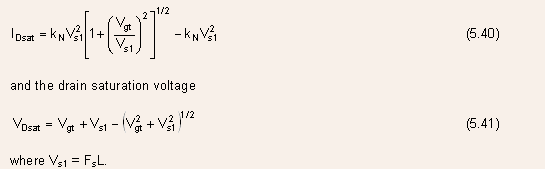
- At very large values of
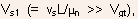 the
term in the brackets in Eq.(5.40) may be expanded into Taylor series,
which gives the following expression for the saturation drain current
for long channel devices:
the
term in the brackets in Eq.(5.40) may be expanded into Taylor series,
which gives the following expression for the saturation drain current
for long channel devices: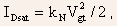 , which does not take into account the velocity saturation effects.
, which does not take into account the velocity saturation effects.
- For long channel devices,
 as
predicted by the constant mobility model, hence, the velocity saturation
effects are not too important for long channel devices.
as
predicted by the constant mobility model, hence, the velocity saturation
effects are not too important for long channel devices.
- Example: assume
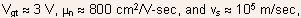 then
for channel length
then
for channel length 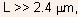 velocity
saturation effects on the drain saturation current may be neglected.
velocity
saturation effects on the drain saturation current may be neglected.
- However, for modern day MOSFETs, the typical gate length is much
smaller than
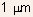 (recently,
Intel has introduced processors using
(recently,
Intel has introduced processors using 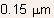 technology),
where the velocity saturation effects are extremely important.
technology),
where the velocity saturation effects are extremely important.
- In the limiting case for short channel devices, when
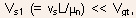 from
Eqs.(5.40) and (5.41), it is seen that
from
Eqs.(5.40) and (5.41), it is seen that 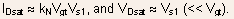
- Note: for short channel device, the drain saturation current is
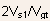 times
smaller than the value predicted by the constant mobility model; and
it becomes linearly dependent on
times
smaller than the value predicted by the constant mobility model; and
it becomes linearly dependent on 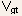 instead
of the familiar square law relation.
instead
of the familiar square law relation.
-
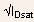 while
plotted as a function of
while
plotted as a function of 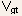 for
a long channel device, shows a linear behavior; however, for short
channel devices, it shows a significant departure from linearity
a measure of whether the device is a short-channel or a long-channel
device.
for
a long channel device, shows a linear behavior; however, for short
channel devices, it shows a significant departure from linearity
a measure of whether the device is a short-channel or a long-channel
device.
-
The drain saturation voltage is also much smaller than that predicted by the constant mobility model.
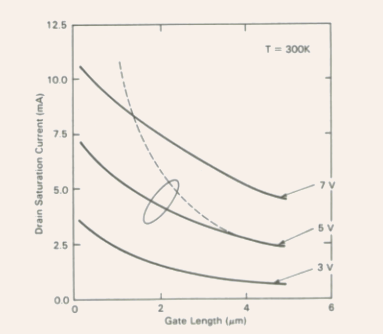
Fig.5.14 The variation of the drain saturation current as a function of the gate length for three different values of the gate voltage (3 V, 5 V, and 7 V). The drain saturation current predicted by the constant mobility model (shown by the dashed line) is also shown for comparison. -
The effects of source/drain series resistance, for these cases, can be accounted for (as done earlier for long channel devices), and the following expressions for the drain saturation current and the drain saturation voltage are obtained:
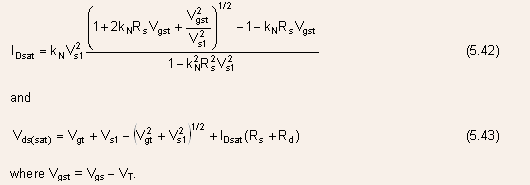
![]() Interpolated Relation
Interpolated Relation
-
The following interpolation formula for the MOSFET I-V characteristic has been proposed by Shur, which describes both limiting cases
 correctly:
correctly:
-
This was one of the earlier formulas, and a huge amount of work has been done in this area for the last ten years or so, in order to further refine the description of the behavior of short-channel MOSFETs.
- In practical devices, the I-V characteristics do not completely
saturate at large drain-to-source voltages, and this is related to
the short channel and other nonideal effects in MOSFETs.
- In order to account for the finite slope of the output characteristics
in saturation, the following modification to the drain current expression
has been proposed:

where
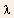 is
referred to as the channel-length modulation parameter (an extremely
important parameter for short channel device a measure of the nonidealities
present in the device)
is
referred to as the channel-length modulation parameter (an extremely
important parameter for short channel device a measure of the nonidealities
present in the device)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |