- Sketch
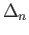 for
for
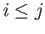 . Show that
. Show that 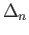 is a compact and connected subspace of
is a compact and connected subspace of
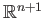 .
.
- Discuss the continuity of the maps (29.1). Prove lemma (29.1). what about the cases
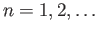 ?
?
- Verify equation (29.8).
- Determine the values of
 (
(
 ) for which
a constant function
) for which
a constant function
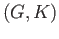 an
an 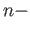 cycle.
cycle.
- Show that the family of all chain complexes forms a category in which the set of morphisms
Mor
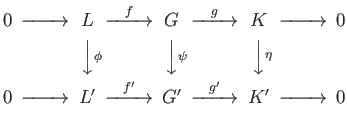 between any two chain
complexes
between any two chain
complexes  and
and  is the set of all chain maps from
is the set of all chain maps from  to
to  .
.
- Naturality of (29.17)-(29.18). Assume given a commutative diagram of chain complexes with exact rows:
Denoting by
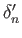 and
and
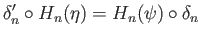 the connecting homomorphisms, sketch relevant diagrams and prove that
the connecting homomorphisms, sketch relevant diagrams and prove that
in
Lecture - XXXI The homology groups and their functoriality
in
Having laid the algebraic foundations in the previous lecture we shall formally define the homology functors
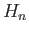 ,
,
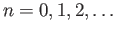 from the category Top to the category AbGr.
We shall discuss
from the category Top to the category AbGr.
We shall discuss 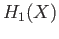 completely and show that
completely and show that 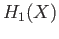 is free abelian of rank equal to the
number of path components of
is free abelian of rank equal to the
number of path components of  .
The groups
.
The groups 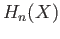 (
(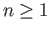 ) vanish when
) vanish when  is a convex subset of
is a convex subset of
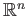 . We shall prove this result
using a technique that would be be considerably generalized in lecture 33. However the special case proved here
for convex subsets would be needed in lecture 33. In the next lecture we shall see
examples of topological spaces
. We shall prove this result
using a technique that would be be considerably generalized in lecture 33. However the special case proved here
for convex subsets would be needed in lecture 33. In the next lecture we shall see
examples of topological spaces  for which
for which 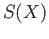 is non-trivial. However
the reader would have to wait till lecture 34 to see more interesting examples.
is non-trivial. However
the reader would have to wait till lecture 34 to see more interesting examples.
Subsections
nisha
2012-03-20
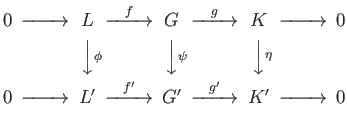 between any two chain
complexes
between any two chain
complexes