Since the standard Euclidean
simplex 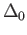 is a singleton, each singular zero simplex
is a singleton, each singular zero simplex
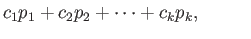 can be identified with a
point of
can be identified with a
point of  namely the image of the singular zero simplex. Thus we may think of a singular zero chain as an element
of the free abelian group generated by the points of
namely the image of the singular zero simplex. Thus we may think of a singular zero chain as an element
of the free abelian group generated by the points of  , that is a formal expression
, that is a formal expression
where
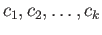 are points of
are points of  and the coefficients
and the coefficients
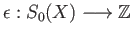 are integers.
are integers.
nisha
2012-03-20