Next: Theorem 31.7: Up: Exercises Previous: Convex sets and barycentric
We consider the standard ![]() simplex
simplex
![]() in
in
![]() with summit
with summit
![]() . The figure below depicts a general point
. The figure below depicts a general point ![]() on the face
on the face
![]() opposite to
opposite to ![]() and
and ![]() an arbitrary point on the line segment joining
an arbitrary point on the line segment joining ![]() and
and ![]() .
The reader may check that if
.
The reader may check that if
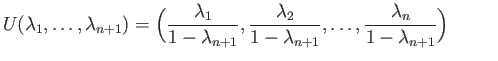 are the barycentric coordinates of
are the barycentric coordinates of ![]() then
the coordinates of
then
the coordinates of ![]() are given by the
are given by the ![]() tuple
tuple