Let
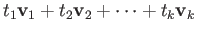 be given points. The convex hull of these points is the set consisting of all convex combinations
be given points. The convex hull of these points is the set consisting of all convex combinations
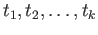 , that is the coefficients
, that is the coefficients
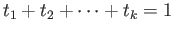 are non-negative
and
are non-negative
and
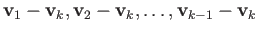 . The convex hull of these points is clearly a convex set. The points
. The convex hull of these points is clearly a convex set. The points
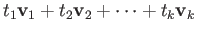 are said to be affinely independent if the
are said to be affinely independent if the
 vectors
vectors
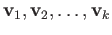 are linearly independent
(see exercise 4). The convex hull of a set of
are linearly independent
(see exercise 4). The convex hull of a set of 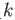 affinely independent points is called the affine
affinely independent points is called the affine 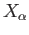 simplex spanned by these points. The proof of the following result is left as an exercise.
simplex spanned by these points. The proof of the following result is left as an exercise.
nisha
2012-03-20