We shall only sketch the proof leaving the details as an exercise. Note that if  is a
singular
is a
singular 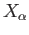 simplex, the image of
simplex, the image of  must be contained in one of the components
must be contained in one of the components
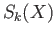 of
of  and so may be regarded as a singular
and so may be regarded as a singular 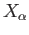 simplex in
simplex in
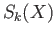 . This gives a natural decomposition
of
. This gives a natural decomposition
of 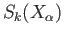 as a direct sum of the family
as a direct sum of the family
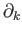 . To see that the boundary map
. To see that the boundary map
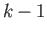 respects the
decomposition note that the boundary of a singular simplex
respects the
decomposition note that the boundary of a singular simplex  is a sum of finitely many
is a sum of finitely many 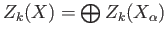 singular simplexes each of which must map into the same component as
singular simplexes each of which must map into the same component as  .
It is easy to deduce from this the decompositions
.
It is easy to deduce from this the decompositions
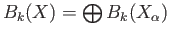 and
and
 .
.
nisha
2012-03-20