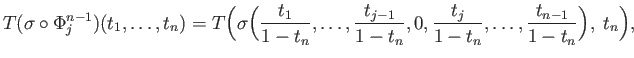Choose a point  and
and
![$ F:X\times [0, 1]\longrightarrow X$](img2398.png) be the homotopy
be the homotopy
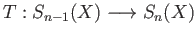 . We shall define a group homomorphism
. We shall define a group homomorphism
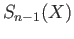 satisfying a
certain property (31.6) below. This is a special case of a chain homotopy that we shall encounter later in a more
general context. Since
satisfying a
certain property (31.6) below. This is a special case of a chain homotopy that we shall encounter later in a more
general context. Since
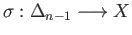 is a free abelian group generated by singular
is a free abelian group generated by singular 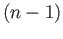 simplicies, it
suffices to define
simplicies, it
suffices to define 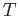 these.
For a singular
these.
For a singular 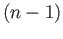 simplex
simplex
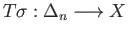 , define the continuous map
, define the continuous map
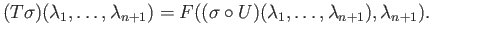 in terms of the barycentric coordinates using the
expression (31.3) namely
in terms of the barycentric coordinates using the
expression (31.3) namely
The continuity of  is left as an exercise.
Let us calculate the boundary of
is left as an exercise.
Let us calculate the boundary of  using equations
(29.1) and (29.4). Recalling the notations used in lecture 29, one checks that
using equations
(29.1) and (29.4). Recalling the notations used in lecture 29, one checks that
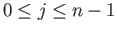
For
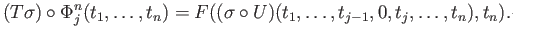 , the
, the 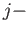 th singular face is given by
th singular face is given by
On the other hand when
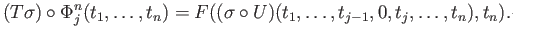 ,
,
which may be rewritten as
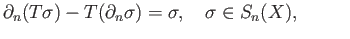 , in agreement with the right hand side of (31.5).
From equation (29.4) it follows that for
, in agreement with the right hand side of (31.5).
From equation (29.4) it follows that for 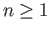 ,
,
whereby we conclude that if
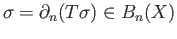 then
then
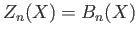 . That is
. That is
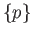 .
nisha
2012-03-20
.
nisha
2012-03-20
![]() , the
, the ![]() th singular face is given by
th singular face is given by