- Prove theorem (31.3).
- Show that for a path connected space
 , every singleton
, every singleton 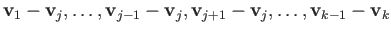 with
with  is a basis for
is a basis for 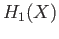 .
.
- Complete the proof of theorem (31.5).
- Show that the set
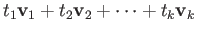 is affinely independent if the
vectors
is affinely independent if the
vectors
are linearly independent for any 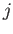 (
(
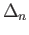 ).
).
- Prove theorem (31.6). Show that the barycentric coordinates are continuous functions of
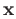 .
All but the
.
All but the 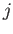 -th barycentric coordinates of
-th barycentric coordinates of 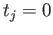 vanish. The set of points in (31.2)
obtained by setting
vanish. The set of points in (31.2)
obtained by setting 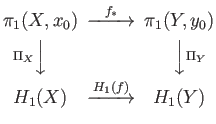 and varying the other coefficients is called the
and varying the other coefficients is called the  th face of the simplex spanned by the given points.
th face of the simplex spanned by the given points.
- Check the continuity of the map
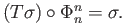 in theorem (31.7).
in theorem (31.7).
in
Lecture - XXXII The abelianization of the fundamental group
in
In this lecture we shall establish a basic result relating the fundamental group
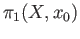 and the first
homology group
and the first
homology group 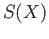 . The result is elegant and states that
. The result is elegant and states that 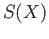 is the abelianization of
is the abelianization of
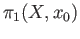 when
when
 is a path connected space.
Further, the abelianization map is natural in the following sense. Suppose that
is a path connected space.
Further, the abelianization map is natural in the following sense. Suppose that
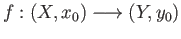 is a continuous map we have the following commutative diagram:
is a continuous map we have the following commutative diagram:
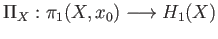
(32.1)
where
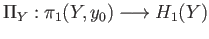 and
and
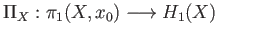 are the quotient maps onto the respective abelianizations.
We shall prove the main theorem (32.1) through a series of lemmas.
are the quotient maps onto the respective abelianizations.
We shall prove the main theorem (32.1) through a series of lemmas.
Subsections
nisha
2012-03-20
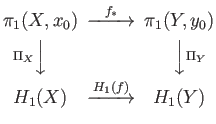 and varying the other coefficients is called the
and varying the other coefficients is called the