Let  be a path connected topological space.
There is a surjective group homomorphism
be a path connected topological space.
There is a surjective group homomorphism
whose kernel is the commutator subgroup
![$ [\pi_1(X, x_0), \pi_1(X, x_0)]$](img2423.png) . Thus
. Thus
Before taking up the proof which will be completed in several steps, we set up the map 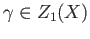 . Note that if
. Note that if
 is a loop in
is a loop in  based at
based at  then
then  is a one cycle, that is to say
is a one cycle, that is to say
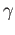 and we denote
its homology class in the quotient
and we denote
its homology class in the quotient 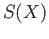 by
by
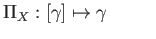 . This suggests that we define
. This suggests that we define
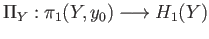 as
as
We shall show that the map is a well-defined surjective group homomorphism and determine its
kernel. We do each of these as a separate lemma. Since homotopy of loops is a map
from the square
![$ [0, 1]\times [0, 1]$](img213.png) whereas a singular two simplex is a map from
whereas a singular two simplex is a map from 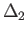 to
to  we must first
set up some standard maps from
we must first
set up some standard maps from 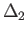 to the square with specific properties. The usual proofs seem slightly
tricky and we shall try an approach that would be useful in the next lecture.
to the square with specific properties. The usual proofs seem slightly
tricky and we shall try an approach that would be useful in the next lecture.
Divide the square
![$ [0, 1]\times [0, 1]$](img213.png) into two triangles by drawing a diagonal from
into two triangles by drawing a diagonal from 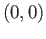 to
to 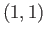 .
Let
.
Let 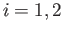 (
(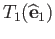 ) be two affine homeomorphisms mapping
) be two affine homeomorphisms mapping 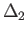 onto the these two triangles given by
onto the these two triangles given by
in
We shall regard the maps 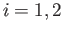 (
(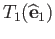 ) as maps from
) as maps from 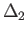 into
into 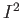 and use them
to prove the following:
nisha
2012-03-20
and use them
to prove the following:
nisha
2012-03-20
![]() into two triangles by drawing a diagonal from
into two triangles by drawing a diagonal from ![]() to
to ![]() .
Let
.
Let ![]() (
(![]() ) be two affine homeomorphisms mapping
) be two affine homeomorphisms mapping ![]() onto the these two triangles given by
onto the these two triangles given by