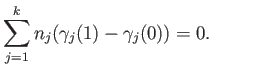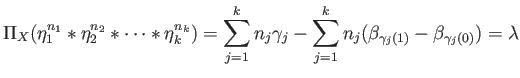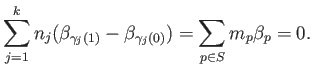Let 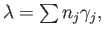 be a singular one cycle say
be a singular one cycle say
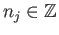 where
where
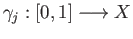 and
and
![$ \gamma_j:[0, 1]\longrightarrow X$](img2465.png) . Since
. Since
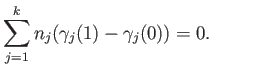
The idea is to complete each of the paths 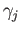 into a loop at
into a loop at  by means of paths joining
by means of paths joining
 to the ends
to the ends
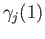 and
and
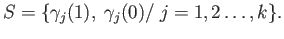 . The only non-trivial part is the book-keeping which
has to be done carefully. Let
. The only non-trivial part is the book-keeping which
has to be done carefully. Let 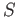 denote the set of endpoints
denote the set of endpoints
For each 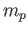 , if
, if 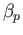 denotes the sum of the coefficients of
denotes the sum of the coefficients of  in (32.7) then
in (32.7) then
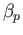 must be zero. Taking a path
must be zero. Taking a path 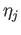 in
in  joining
joining  and
and 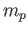 we construct for each
we construct for each 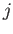 a loop
a loop 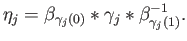 in
in  based at
based at  namely,
namely,
Finally
since
nisha
2012-03-20