Let 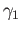 and
and 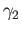 be two homotopic loops based at
be two homotopic loops based at 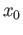 and let
and let
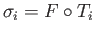 be the homotopy fixing the base point
be the homotopy fixing the base point 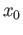 . Then
. Then
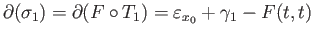 (
(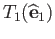 ) are two singular two
simplicies. It is an exercise to compute the boundary of these two singular simplicies and we find easily
) are two singular two
simplicies. It is an exercise to compute the boundary of these two singular simplicies and we find easily
The one chain
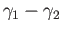 is the boundary of the two chain
is the boundary of the two chain
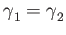 whence
whence
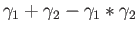 .
.
nisha
2012-03-20