Let 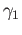 and
and 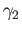 be two loops in
be two loops in  based at
based at  . We have to show that the one chain
. We have to show that the one chain
is a boundary of some singular two chain  . The idea behind the construction is simple.
We first define a map
. The idea behind the construction is simple.
We first define a map
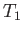 whose restrictions to the four sides of the square are
whose restrictions to the four sides of the square are
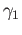 ,
, 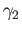 ,
,
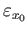 and
and
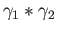 . As in the previous lemma we shall employ
the maps
. As in the previous lemma we shall employ
the maps 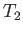 ,
, 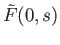 to construct our two chain
to construct our two chain  .
.
We proceed as in lecture 7 by defining
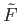 from the boundary of
from the boundary of 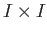 to
to ![$ [0, 1]$](img13.png) , using Tietze's
theorem to extend it to the whole of
, using Tietze's
theorem to extend it to the whole of 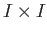 and then composing with
and then composing with
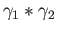 . So we define
. So we define
and extend it continuously to 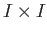 . Let
. Let
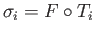 be given by
be given by
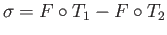 The figure below depicts
The figure below depicts 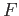 along the boundary of
along the boundary of 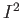 :
:
in
It is now an easy matter to verify that the boundary of the two chain  given by
given by
is the one chain
Now, if
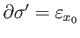 be the constant map taking value
be the constant map taking value  then
then
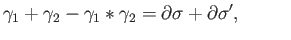 whereby we conclude that
whereby we conclude that
which implies
![$ \Pi_{X}([\gamma_1][\gamma_2]) = \Pi_X([\gamma_1*\gamma_2]) = \Pi_X([\gamma_1]) + \Pi_X([\gamma_2])$](img2461.png) .
.
 nisha
2012-03-20
nisha
2012-03-20
![]() from the boundary of
from the boundary of ![]() to
to ![]() , using Tietze's
theorem to extend it to the whole of
, using Tietze's
theorem to extend it to the whole of ![]() and then composing with
and then composing with
![]() . So we define
. So we define
![]() given by
given by