Given a pair of
functors
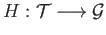 and
and
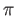 , a natural
transformation
, a natural
transformation 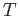 between
between 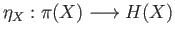 and
and 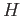 is a function
which assigns to each object
is a function
which assigns to each object 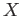 of
of 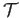 a
morphism
a
morphism
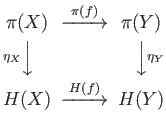 such that for each morphism
such that for each morphism
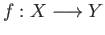 in
in 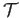 , the following diagram commutes
, the following diagram commutes
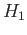
(32.12)
The notation used in this definition is quite suggestive.
The Poincaré-Hurewicz map provides a natural transformation between the functors 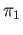 and
and 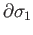 .
.
nisha
2012-03-20
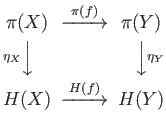 such that for each morphism
such that for each morphism